Некоторые примеры заданий по теме лекции

Пример 1. Сделать прямой и обратный ход метода Гаусса по расширенной матрице:

.

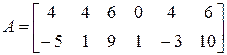Заметим, что матрица расширена за счет присоединения к матрице

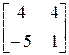
четырех правых частей:

, , , .

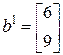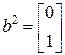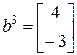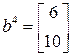Прямой ход метода Гаусса.

На первом шаге прямого хода из второй строки вычитаем первую, умноженную на коэффициент :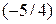

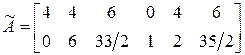
В результате получаем четыре, эквивалентные исходным, СЛАУ с верхней треугольной матрицей. Для их решения применим обратный ход.

Обратный ход метода Гаусса.

1)

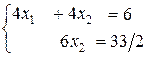
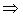
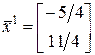
2)

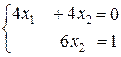
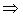
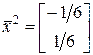
3)

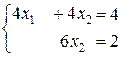
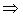
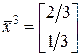
4)

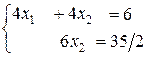
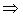
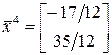
Пример 2. Дана краткая формулировка СЛАУ:

,

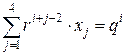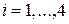
Представить заданную СЛАУ в матрично-векторной форме.

,

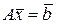где

, , .

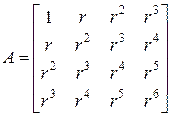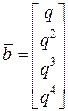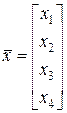Пример 3. Дана матрица :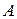

.

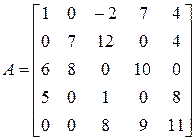Сформулировать СЛАУ относительно 4-го столбца обратной матрицы .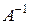

Матрично-векторная формулировка:

,

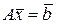где

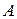– заданная матрица,

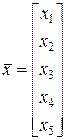– вектор неизвестных значений 4-го столбца ,

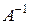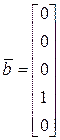– вектор правой части.