Рисунок 13.6
Рисунок 13.5
Рисунок 13.4
Рисунок 13.3
Рисунок 13.2
Рассмотрим более подробно график 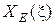 : 1) в области малых расстроек
: 1) в области малых расстроек 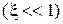 ,
, 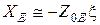 , т.е. это прямая с отрицательным наклоном; 2) при
, т.е. это прямая с отрицательным наклоном; 2) при 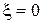
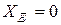 ; 3) в области больших расстроек
; 3) в области больших расстроек 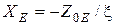 , т.е. это гипербола; 4) при
, т.е. это гипербола; 4) при 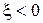
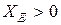 , ведь на низких частотах
, ведь на низких частотах 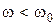 характер реактивности определяет индуктивная ветка; при
характер реактивности определяет индуктивная ветка; при 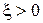
 , ведь на частотах
, ведь на частотах 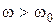 характер реактивности сопротивления
характер реактивности сопротивления 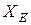 определяется емкостью.
определяется емкостью.
13.2 Токи и напряжения в параллельном контуре.
Векторная диаграмма токов
Рассмотрим параллельный контур вида (рис.13.1б). Найдем токи веток 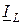 ,
, 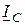 и напряжение на контуре
и напряжение на контуре 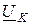 , считая известным ток общей ветки
, считая известным ток общей ветки  . Расчет сделаем для комплексных действующих значений.
. Расчет сделаем для комплексных действующих значений.
Согласно закону Ома  ;
; 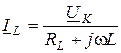 ;
; 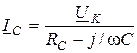 .
.
На частоте резонанса 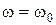 выполняются соотношения:
выполняются соотношения: 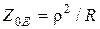 ;
;  . Тогда резонансные значения токов и напряжения будут такими:
. Тогда резонансные значения токов и напряжения будут такими: 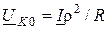 ;
;
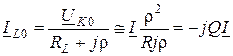 ;
;  . (13.5)
. (13.5)
Поскольку действующее (амплитудное) значение токов в ветках контура в Q раз превышает действующее (амплитудное) значение тока в общей ветке, резонанс в параллельном контуре носит название резонансном токов.
Итак, резонанс токов - явление резонанса на участке электрической цепи, которая имеет параллельно соединенные индуктивные и емкостные элементы.
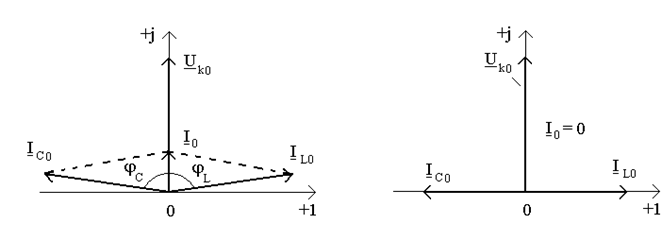
Соответственно к найденным выражениям на рис.13.3 приведено векторную диаграмму токов и напряжения в параллельном контуре.
 а) б)
а) б)
Диаграмма (рис.13.3а) изображенная для случая, когда 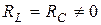 . В таком случае фазовые углы
. В таком случае фазовые углы 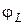 и
и 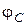 близки к значению 90°, но не равняются ему:
близки к значению 90°, но не равняются ему: 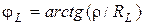 ;
; 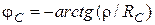 . Общий ток по величине весьма мал, а по фазе совпадает с напряжением
. Общий ток по величине весьма мал, а по фазе совпадает с напряжением 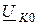 . При резонансе выполняется соотношение
. При резонансе выполняется соотношение 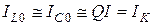 . Ток
. Ток 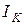 называют током контура.
называют током контура.
Векторная диаграмма (рис.13.3б) соответствует идеальному контуру без потерь (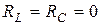 ), который настроен в резонанс. В таком случае токи
), который настроен в резонанс. В таком случае токи 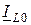 и
и 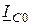 точно равняются друг другу и противоположны по фазе:
точно равняются друг другу и противоположны по фазе:  . Поэтому ток в неразветвленном участке цепи равняется нулю. Но при этом в самом контуре циркулирует ток
. Поэтому ток в неразветвленном участке цепи равняется нулю. Но при этом в самом контуре циркулирует ток 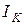 .
.
13.3 Резонансные кривые параллельного контура
Перейдем от полученных выше частотных характеристик входного сопротивления (13.3) к характеристике напряжения на контуре. Будем считать, что действующее значение тока, который питает контур, неизменно: I = const. Такая ситуация эквивалентна питанию контура генератором тока (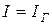 ,
, 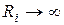 ). Комплексное действующее значение напряжения на контуре:
). Комплексное действующее значение напряжения на контуре: 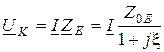 .
.
Если I=const, напряжение на контуре зависит от частоты так же, как входное сопротивление (с точностья до постоянного коэффициента). Тогда резонансная кривая напряжения на контуре будет такой:
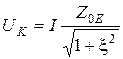 . (13.6)
. (13.6)
Уравнения резонансных кривых токов находим из выражения (13.5) при условии, что добротность контура достаточно высокая (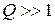 ,
,  ):
):
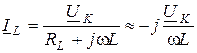 ;
;  ; (13.7)
; (13.7)
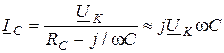 ;
; 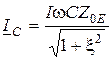 . (13.8)
. (13.8)
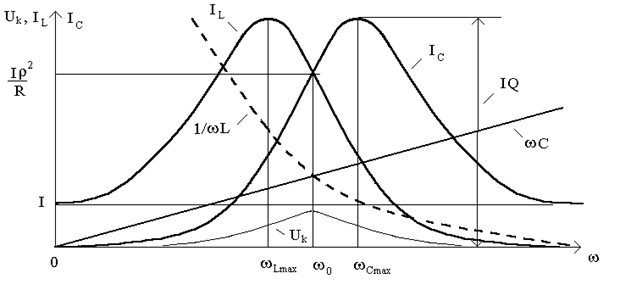
Проанализируем полученное выражения и соответствующие графики (рис.13.4):
1) Поскольку кривая 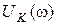 является симметричной, а кривая тока
является симметричной, а кривая тока 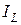 получена умножением на проводимость
получена умножением на проводимость 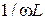 , то максимум
, то максимум 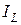 смещается в сторону частот, меньших чем резонансная (
смещается в сторону частот, меньших чем резонансная (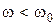 );
);
2) при 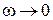
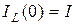 (рис.13.5,а); при
(рис.13.5,а); при 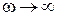
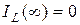 (рис.13.5б).
(рис.13.5б).
3) Поскольку кривая 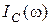 получена умножением симметричной кривой
получена умножением симметричной кривой 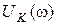 на проводимость
на проводимость 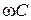 , то максимум кривой
, то максимум кривой 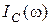 смещается в сторону частот, больших чем резонансная (
смещается в сторону частот, больших чем резонансная (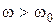 ). Граничные значения тока
). Граничные значения тока 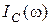 такие:
такие:  (рис.13.5а);
(рис.13.5а); 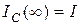 (рис.13.5б).
(рис.13.5б).
а) б)
13.4 Влияние внутреннего сопротивления генератора и сопротивления нагрузки на выборочные свойства параллельного контура
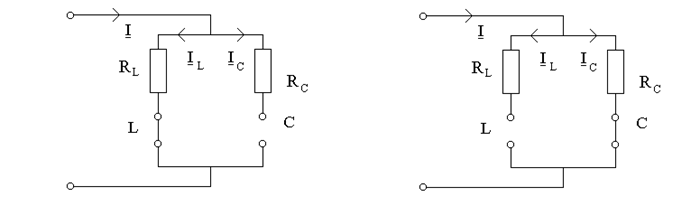
При реальных условиях, когда контур питается реальным генератором, ток I изменяется со сменой напряжения на контуре. Это может существенно повлиять на вид частотных характеристик. В этом случае для исследования выборочных свойств контура следует заменить источник питания эквивалентной схемой с идеальным источником тока (рис.13.6).
Цепь (рис.13.6б) можно рассматривать как некоторый контур, который шунтируется активным сопротивлением 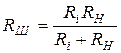 и питается в точках 1-1' постоянным током
и питается в точках 1-1' постоянным током 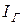 .
.
Если сопротивление 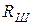 , которое подключено параллельно контуру, пересчитать в последовательное сопротивление
, которое подключено параллельно контуру, пересчитать в последовательное сопротивление 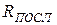 по формуле (12.10), добротность эквивалентного контура (по правую сторону точек 1-1') будет представлять
по формуле (12.10), добротность эквивалентного контура (по правую сторону точек 1-1') будет представлять
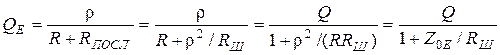 , (13.9)
, (13.9)
где 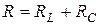 .
.
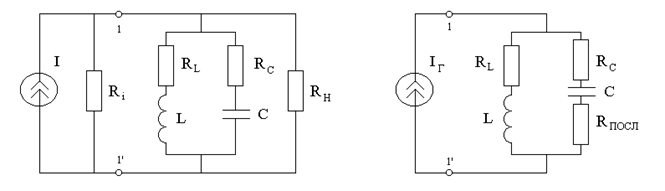
а) б)
Эквивалентная добротность 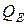 зависит от собственной добротности
зависит от собственной добротности 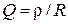 и от соотношения сопротивления
и от соотношения сопротивления 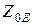 и внутреннего сопротивления генератора
и внутреннего сопротивления генератора 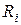 (или сопротивления нагрузки
(или сопротивления нагрузки 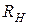 , или
, или 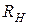 и
и 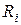 вместе). С уменьшением
вместе). С уменьшением 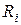 (
(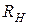 ) эквивалентная добротность уменьшается, т.е. полоса пропускания увеличивается:
) эквивалентная добротность уменьшается, т.е. полоса пропускания увеличивается:  .
.
Уравнение резонансной кривой напряжения с учетом влияния 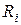 (
(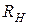 ) будет иметь вид:
) будет иметь вид:
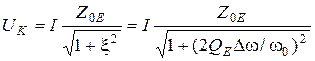 .
.
Эта характеристика приближается к идеальной резонансной кривой (13.6) лишь при 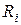
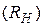
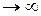 . Если же
. Если же  и контур питается от источника напряжения с ЭДС E, напряжение на контуре вобщем не зависит от частоты, она остается равной значению ЭДС источника E.
и контур питается от источника напряжения с ЭДС E, напряжение на контуре вобщем не зависит от частоты, она остается равной значению ЭДС источника E.
Итак, в отличии от последовательного контура, использование параллельного резонансного контура необходимо с точки зрения выборочности тольки в том случае, когда внутреннее сопротивление генератора тока достаточно большое 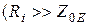 ).
).
 2014-02-09
2014-02-09 1703
1703








