ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 1
Примеры решения задач
Найти изображение заданной функции:
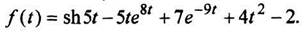
РЕШЕНИЕ
Так как оригинал - алгебраическая сумма функций, то для изображения используем линейные свойства изображения (формула (3)) и таблицу преобразований Лапласа.
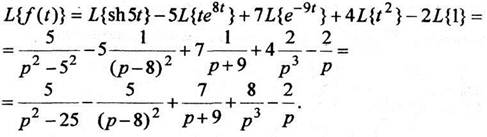
Оригинал по заданному изображению можно определить так, как это сделано в примере 10 или в примере 11.
5.3. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 3
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:
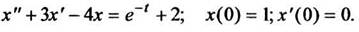
РЕШЕНИЕ
Введем обозначения 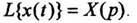 Преобразуем обе части
Преобразуем обе части
дифференциального уравнения по Лапласу. С учетом линейных свойств преобразования, формул (5), (6) и таблицы 1 преобразований Лапласа, получим:
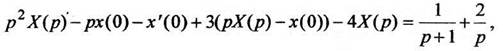
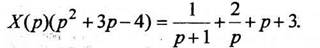
Решим уравнение относительно 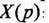
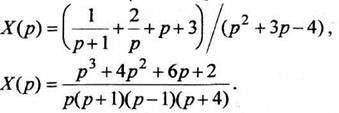
Для нахождения оригинала используем теорему разложения (11-14); особые точки функции 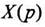 - простые полюсы
- простые полюсы 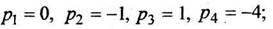
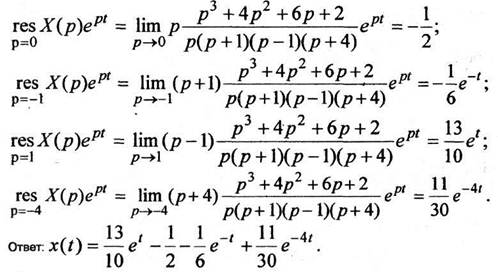
 5.4 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 4
5.4 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 4
Решить систему дифференциальных уравнений:
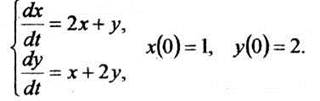
РЕШЕНИЕ
Введём обозначения: 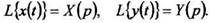 Преобразуем систему уравнений по Лапласу:
Преобразуем систему уравнений по Лапласу:
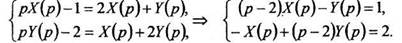
Решаем полученную систему алгебраических уравнений методом Крамера.
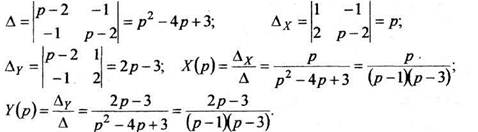
Теперь по изображениям 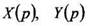 определяем оригиналы
определяем оригиналы 
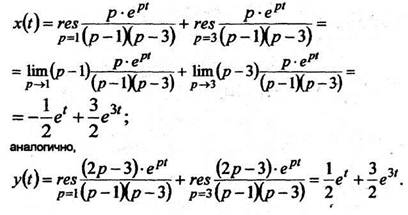
 2014-02-09
2014-02-09 940
940







