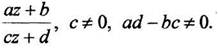1. Функции комплексной переменной 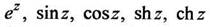 определяются как суммы следующих рядов, сходящихся во всей плоскости комплексного переменного:
определяются как суммы следующих рядов, сходящихся во всей плоскости комплексного переменного:
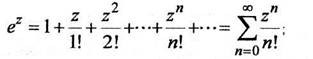 (1.4)
(1.4)
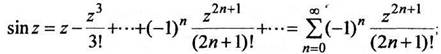 (1.5)
(1.5)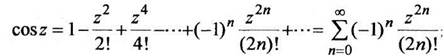 (1.6)
(1.6)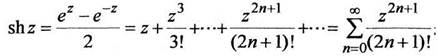 (1.7)
(1.7)
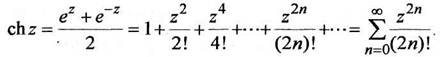 (1.8)
(1.8)
Из определения функций (10.4)-(10.8) следуют формулы, связывающие их:
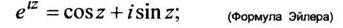 (1.9)
(1.9)
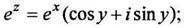 (1.10)
(1.10)
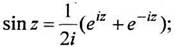 (1.11)
(1.11)
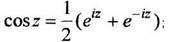 (1.12)
(1.12)
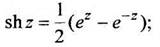 (1.13)
(1.13)
 (1.14)
(1.14)
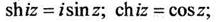 (1.15)
(1.15)
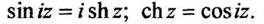 (1.16)
(1.16)
Элементарные функции (1.4) – (1.8) являются однозначными и непрерывными на всей комплексной области Z.
2. Показательная функция 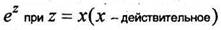 совпадает с обычной функцией
совпадает с обычной функцией 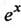 для нее справедлива теорема сложения
для нее справедлива теорема сложения 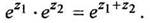
Функция 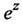 периодическая с чисто мнимым основным периодом
периодическая с чисто мнимым основным периодом
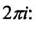
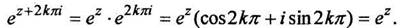
Тригонометрические функции 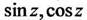 для действительных
для действительных 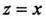 совпадает с обычным синусом и косинусом, периодичны с действительным периодом
совпадает с обычным синусом и косинусом, периодичны с действительным периодом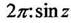 - нечетная,
- нечетная, 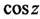 - четная функция; подчиняются обычным тригонометрическим соотношениям:
- четная функция; подчиняются обычным тригонометрическим соотношениям:
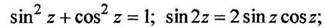 и т.п.
и т.п.
Функция 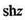 называется гиперболическим синусом; функция
называется гиперболическим синусом; функция 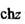 называется гиперболическим конусом. Гиперболические функции
называется гиперболическим конусом. Гиперболические функции 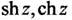 выражаются через тригонометрические функции формулами (1.15,1.16).
выражаются через тригонометрические функции формулами (1.15,1.16).
С помощью функций (1.4) - (1.8) вводятся другие элементарные функции. 3 Логарифмическая функция определяется как функция, обратная показательной:
если: 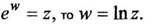
Для нее справедливо свойство логарифмов:
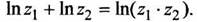 |
В частности, полагая 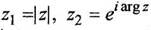 , получаем
, получаем
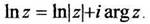 (1.17)
(1.17)
В формуле (1.17) символ 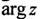 может обозначать любое значение аргумента, поэтому каждое комплексное число имеет бесчисленное множество логарифмов.
может обозначать любое значение аргумента, поэтому каждое комплексное число имеет бесчисленное множество логарифмов.
Выражение 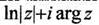 называется главным значением логарифмической функции и обозначается, как
называется главным значением логарифмической функции и обозначается, как  Многозначная логарифмическая функция обозначается
Многозначная логарифмическая функция обозначается 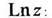
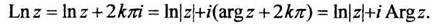 (1.18)
(1.18)
4. Общая показательная функция:
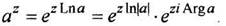 (1.19)
(1.19)
Эта функция представляет собой совокупность отдельных, не связанных между собой однозначных функции, отличающихся множителями 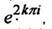 где k- целое число. Главное значение этой многозначной функции равно
где k- целое число. Главное значение этой многозначной функции равно 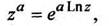
где 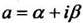 - произвольное комплексное число.
- произвольное комплексное число.
Полагая, 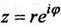 , получаем
, получаем 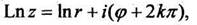
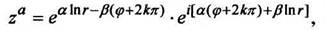 (1.20)
(1.20)
где 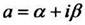 - произвольное комплексное число.
- произвольное комплексное число.
Полагая 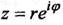 , получаем
, получаем 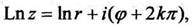
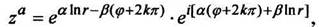 (1.21)
(1.21)
где k – целое число. При 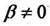 функция
функция 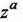 всегда имеет бесконечно много значений.
всегда имеет бесконечно много значений.
Если 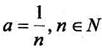 , то получаем многозначную функцию - корень n-й степени
, то получаем многозначную функцию - корень n-й степени 
При 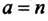 имеем частный случай однозначной степенной функции
имеем частный случай однозначной степенной функции 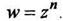
К основным элементарным функциям комплексной переменной относится также дробно-рациональная функция и её частные случаи.
Дробно-рациональная функция:
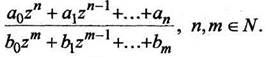 (1.22)
(1.22)
Частные случаи этой функции:
а)линейная функция 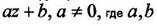 - комплексные числа
- комплексные числа
б)степенная функция 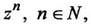
 2014-02-09
2014-02-09 3688
3688