Пусть функция 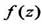 определена в некоторой окрестности точки Z. Функция дифференцируема в точке Z, если существует предел.
определена в некоторой окрестности точки Z. Функция дифференцируема в точке Z, если существует предел.
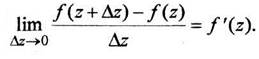
Этот предел называется производной функции 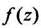 в точке Z. Функция дифференцируемая в каждой точке области D и имеющая в этой области непрерывную производную
в точке Z. Функция дифференцируемая в каждой точке области D и имеющая в этой области непрерывную производную 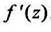 называется аналитической в области D.
называется аналитической в области D.
Функция 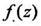 аналитическая в точке,
аналитическая в точке, 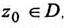 если
если 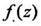 является аналитической в некоторой окрестности точки Z0.
является аналитической в некоторой окрестности точки Z0.
Для того чтобы функция 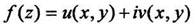 была аналитической в области D, необходимо и достаточно одновременное существование в этой области непрерывных частных производных функций
была аналитической в области D, необходимо и достаточно одновременное существование в этой области непрерывных частных производных функций 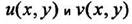 удовлетворяющим условиям Коши-Римана:
удовлетворяющим условиям Коши-Римана:
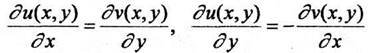 (1.2)
(1.2)
При выполнении условий (2) производная 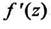 может быть вычислена по одной из формул
может быть вычислена по одной из формул
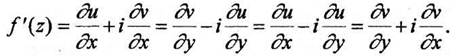 (1.3)
(1.3)
Для аналитических функций правила дифференцирования и таблица производных элементарных функций комплексной переменной такие же, как для функций действительной переменной, что иллюстрирует следующий пример. Пример 3, Проверить выполнение условий Коши-Римана для функции 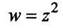 является дифференцируемой и аналитической на всей комплексной плоскости Z:
является дифференцируемой и аналитической на всей комплексной плоскости Z:
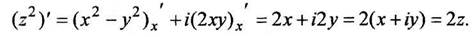
Таким образом, 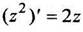
 2014-02-09
2014-02-09 2791
2791








