Астатическая система стабилизации угла крена

Астатизм в системе обеспечивается путем введения интеграла от ошибки

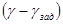
в закон управления, который принимает следующий вид

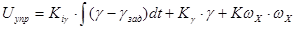
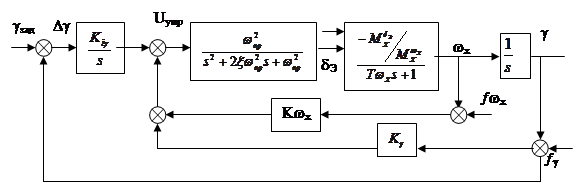
На рис. ниже показана структурная расчетная схема системы

ПФ замкнутой системы

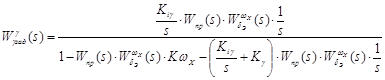
Или

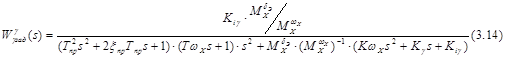
Введение сигнала ОС по углу крена 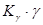обеспечивает структурную устойчивость системы стабилизации, так как в противном случае необходимые условия устойчивости не будут выполняться при любых значениях , .

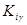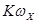Устойчивость системы.

Области устойчивости в плоскости параметров k_γ и k_ωx (при 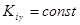) для нескольких значений частоты привода 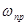и двух значений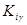

По сравнению с областью устойчивости статической системой в астатической сместилась вправо ее левая граница, уменьшив тем самым область устойчивости. Отличительная особенность – с введение интеграла и ростом 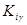левая граница проходит выше оси OK_g и, следовательно, ОС по w_x становится также функционально необходимой по условиям устойчивости.

Правая граница области устойчивости определяется в основном быстродействием привода.

Статические ошибки. Введение интеграла в закон управления (см.3.13) позволяет устранить статические ошибки стабилизации, кроме ошибки из-за погрешности измерения угла крена ¦_g - невозможно точно управлять координатой, если она измеряется с ошибкой.

Динамические характеристики системы. В качестве исходной математической модели замкнутой системы допустимо использовать упрощенную в предположении, что привод безынерционен. В этом случае ПФ (3.14) принимает вид

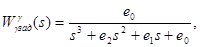
где

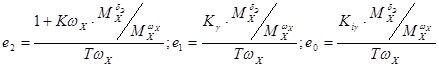
Динамические характеристики системы такой системы полностью определяются коэффициентами характеристического многочлена , которые можно формировать желаемым образом с помощью передаточных чисел закона управления (3.13). При этом удобно использовать метод стандартных коэффициентов для ПФ, записанной в форме Вышнеградского

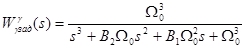
где 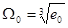нормированная собственная частота системы. На основании (3.15) получаем следующие выражения

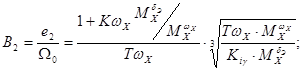
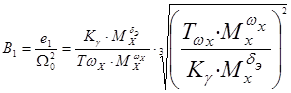
Коэффициенты Вышнеградского В₁, В₂ характеризуют форму переходного процесса путем задания желаемого распределения полюсов, а нормированная собственная частота системы W₀ - его длительность, определяемую с помощью формулы

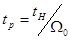
где t_н - время регулирования нормированного переходного процесса. Задаваясь желаемыми коэффициентами В₁, В₂ исходя из обеспечения заданных требований к времени регулирования t_p и перерегулированию s <5% на основании (3.17) получают расчетные выражения для передаточных чисел системы стабилизации.