Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

Пусть дана квадратичная форма 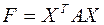, Поскольку – симметрическая матрица, для нее существует диагонализирующая ортогональная матрица 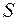, такая что

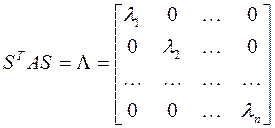
где 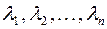– собственные значения матрицы .

Применим к квадратичной форме линейное преобразование ,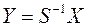

где 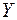– матрица-столбец новых переменных ;

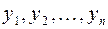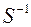– матрица, обратная к .

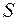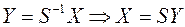
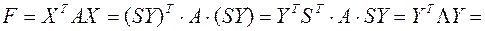
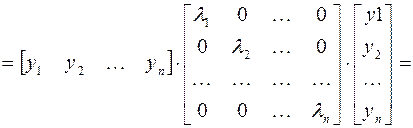
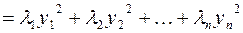
Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1 или –1, т.е. квадратичная форма имеет вид 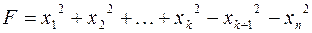. Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу 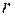квадратичной формы.