Теорема. Если 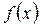 непрерывна на отрезке
непрерывна на отрезке 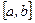 , дифференцируема во всех внутренних точках этого отрезка и
, дифференцируема во всех внутренних точках этого отрезка и 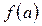 =
=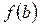 (т.е. принимает на концах этого отрезка равные значения), то внутри этого отрезка существует хотя бы одна точка
(т.е. принимает на концах этого отрезка равные значения), то внутри этого отрезка существует хотя бы одна точка 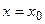 , для которой
, для которой 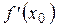 =0.
=0.
Доказательство.
Если 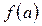 =
=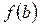 , то возможны два случая:
, то возможны два случая:
1. функция 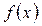 = const внутри
= const внутри 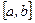
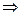
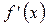 = 0, "
= 0, " 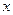 Î
Î 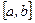 .
.
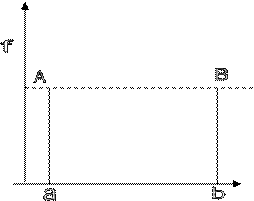
2. функция изменяется, т.к. 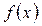 непрерывна на
непрерывна на 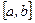
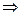 она принимает на
она принимает на 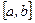 свое наибольшее и наименьшее значения, причем хотя бы одно из них будет внутри интервала
свое наибольшее и наименьшее значения, причем хотя бы одно из них будет внутри интервала 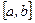 .
.
По условию функция дифференцируема во всех точках 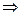 и в точке, где принимается наибольшее (наименьшее) значение (
и в точке, где принимается наибольшее (наименьшее) значение (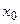 )
) 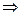 по теореме Ферма
по теореме Ферма 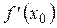 =0.
=0.
 |
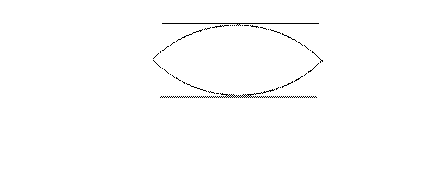
Если 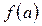 =
=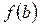 =0
=0 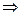 между всякими двумя нулями функции лежит точка
между всякими двумя нулями функции лежит точка 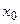 , что
, что 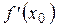 =0 (именно в таком виде теорема дана Роллем).
=0 (именно в таком виде теорема дана Роллем).
Теорема Роля теряет силу, если не требовать дифференцируемость во всех точках интервала.
Пример 1. 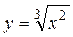 , при
, при 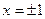 ,
, 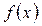 =1, но
=1, но 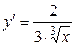 ни где не обращается в 0, в точке
ни где не обращается в 0, в точке 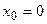
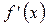 не существует.
не существует.

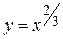
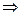
 .
.
 2014-02-09
2014-02-09 430
430








