Основные теоремы дифференциального исчисления. Применение дифференциального исчисления к исследованию функций

Применение дифференциального исчисления к исследованию функций.

Основные теоремы дифференциального исчисления. 2

Теорема Ферма. 2

Теорема Ролля. 3

Теорема Лагранжа (о конечных приращениях). 4

Теорема Коши (об отношении приращений двух функций). 6

Предел отношения двух бесконечно малых (Правило Лопиталя). 7

Применение дифференциального исчисления к исследованию функций.

Теорема Ферма.

Теорема. Пусть 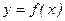непрерывна на 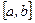и принимает наибольшее (наименьшее) значение во внутренней точке 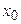этого интервала .

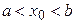Пусть для 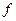в точке $ .

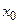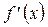
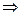
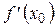Доказательство.

Если 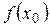- наибольшее значение .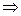

.

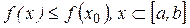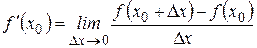Рассмотрим отношение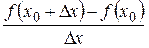

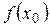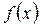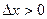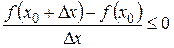
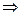
1). Числитель меньше 0, т.к. - наибольшее значение Þ при , 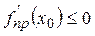(правая производная).

2). При .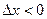

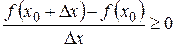
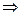
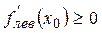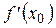
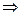
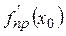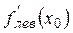
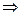
Так как по условию $ ==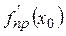==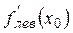 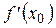0.

Доказательство для 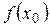наименьшего значения 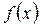– аналогично.

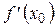
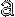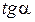= = 0, т.к. 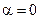касательная || .

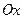Если наибольшие и наименьшие значения принимаются на концах интервала, то производная не обязательно равна нулю и касательная не обязательно параллельна Ox.

Из теоремы Ферма вытекает теорема Ролля.