Теорема. Если 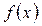 непрерывна на отрезке
непрерывна на отрезке 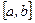 и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка
и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка 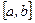 найдется по крайней мере одна точка
найдется по крайней мере одна точка 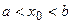 , что
, что
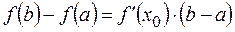 .
.
Доказательство:

Введем вспомогательную функцию  , где
, где 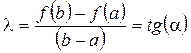 . Функция
. Функция 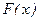 удовлетворяет всем условиям теоремы Роля: непрерывна на
удовлетворяет всем условиям теоремы Роля: непрерывна на 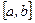 , дифференцируема на
, дифференцируема на 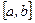 и на концах интервала
и на концах интервала 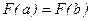 :
:
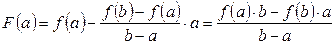
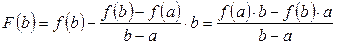 .
.
По теореме Ролля хорда, стягивающая конечные точки дуги этой функции (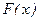 ) будет || оси
) будет || оси 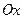 и $ точка
и $ точка 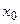 , что
, что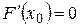 .
.
Но 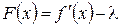
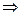
 =0
=0 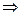
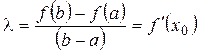
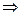
Т. 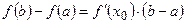 - это формула конечных приращений.
- это формула конечных приращений.
Приращение функции на 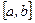 равно производной в некоторой точке этого интервала умноженное на приращение аргумента.
равно производной в некоторой точке этого интервала умноженное на приращение аргумента.
Геометрический смысл. Если во всех точках дуги АВ существует касательная, то найдется такая точка 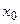 , в которой касательная параллельна хорде.
, в которой касательная параллельна хорде.
 2014-02-09
2014-02-09 1606
1606








