Пример 1. 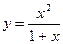
I. Функция определена и непрерывна при всех 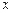 , исключая
, исключая 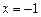 (бесконечный разрыв):
(бесконечный разрыв):
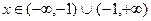 Þ
Þ 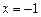 - вертикальная асимптота (
- вертикальная асимптота (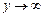 ).
).
3). При этом (поведение в окрестности точки разрыва):
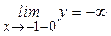 ,
,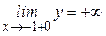
4). 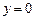 только при
только при 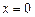 из решения уравнений
из решения уравнений 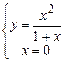 и
и 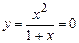
II. 1). Ищем точки экстремума, т. е. 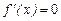 .
.
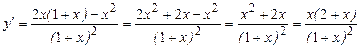
Экстремумы: 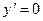 или не существует
или не существует

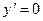 Þ
Þ 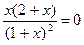 Þ
Þ 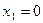 ,
, 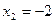 , при
, при 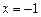
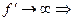 не существует
не существует
2). Интервалы монотонности
| (-¥; -2) | 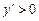
| 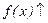
|
Þ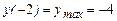
|
| (-2; -1) | 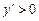
| 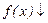
| |
| (-1; 0) | 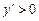
| 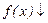
|
Þ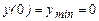
|
| (0; ¥) | 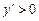
| 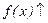
|
3). Экстремальные значения функции:
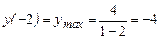 .
.
III. Интервалы выпуклости и вогнутости:
Для нахождения интервалов выпуклости и вогнутости вычислим 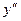 .
.
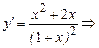
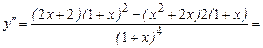
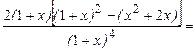
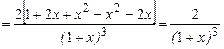
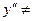 0 нигде. Не существует при
0 нигде. Не существует при 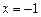
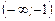
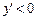 ,
, 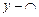
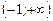
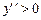 ,
, 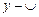
Þ 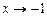 ,
, 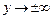 ,
,
т.е. точекперегиба нет, 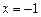 - точка разрыва,
- точка разрыва,
при 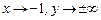
IV. Поведение на бесконечности ¥. Наклонные асимптоты.
1).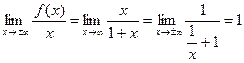 Þ
Þ 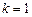 .
.
2).
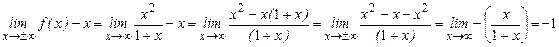
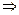
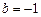
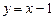 – наклонная асимптота.
– наклонная асимптота.
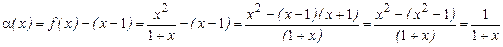
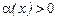 , при
, при 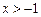 ,
, 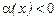 , при
, при 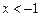 Þ
Þ
при 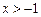
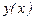 расположена над асимптотой,
расположена над асимптотой,
при 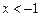
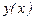 - под асимптотой.
- под асимптотой.
 |
 2014-02-09
2014-02-09 341
341







