Лекция 2 линейные дифференциальные уравнения высших порядков

Определение 1. Линейным дифференциальным оператором называется оператор вида

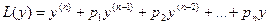, (1)

где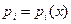, 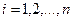определены и непрерывны на некотором интервале.

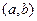Линейный дифференциальный оператор ставит в соответствие функции 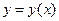новую функцию 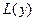, определенную по формуле (1).

Свойства линейного дифференциального оператора:

1. 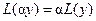, где 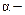постоянная.

▲. ■

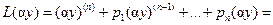
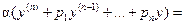
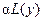2.

▲

==. ■

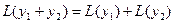
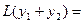
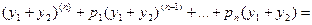
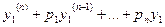
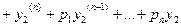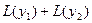Определение 2. Линейным однородным дифференциальным уравнением называется уравнение вида 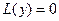, или

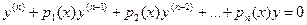. (2)

Свойства решений линейного однородного дифференциального уравнения.

1. Если 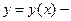решение уравнения (14.2), а 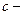произвольная постоянная, то 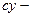тоже решение уравнения (2).

▲ Согласно свойству 1 линейного дифференциального оператора, . ■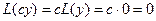

2. Есл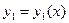и и 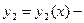решения уравнения (2), то 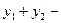тоже решение уравнения (2).

▲ Согласно свойству 2 линейного дифференциального оператора, . ■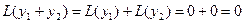

3. Если 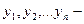решения уравнения (2), а 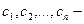произвольные постоянные, то 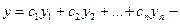тоже решение уравнения (2).

▲ Это свойство является очевидным следствием свойств 1 и 2. ■

Функция 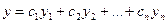зависит 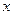от и от 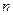произвольных постоянных. При любых значениях этих постоянных она является решением уравнения (2). Ниже будут изучаться условия, при которых эта функция является общим решением уравнения (2). т.е. условия, при которых она удовлетворяет определению 7 предыдущей лекции.

Линейная зависимость и независимость функций

Определение 3. Функции 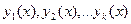называются линейно зависимыми на некотором множестве 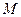, если существуют постоянные 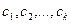, хотя бы одна из которых отлична от нуля, такие, что

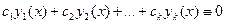(3)

(здесь знак тождества «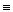» означает выполнение равенства (14.3) для 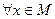). Функции 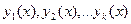называются линейно независимыми на множестве 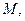если тождество (3) выполняется только при всех коэффициентах .

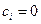Пример 1. Покажем, что функции 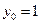, , 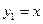, 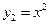…, 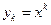линейно независимы на любом конечном или бесконечном промежутке .

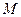▲ Из равенства

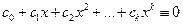(4)

следует, что любой 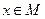является корнем уравнения (4). Но любой многочлен степени 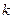имеет только 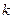корней, откуда следует, что единственным возможным является случай . ■

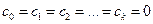Пример 2. Покажем, что функци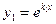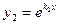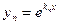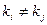и,, …,,при 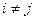, линейно независимы на любом конечном или бесконечном промежутке .

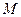▲ Пусть

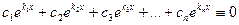. (5)

Докажем, что в равенстве (5) все коэффициенты 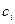обязательно равны 0, например, докажем, что 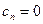. Разделим (5) на :

.

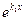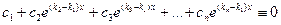Дифференцируем это равенство по :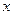

.

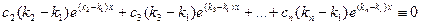Разделим последнее равенство на 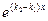, учитывая, что :

.

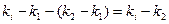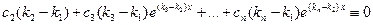Теперь дифференцируем это равенство по 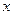и так далее. В итоге получим:

.

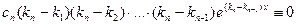В этом равенстве все сомножители, кроме первого, отличны от 0, отсюда . ■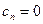

Линейно зависимые и линейно независимые функции обладают обычными свойствами линейно зависимых и линейно независимых векторов.

Кроме того, оказывается, что линейная зависимость и независимость функций тесно связана с так называемым определителем Вронского.

Определение 4. Пусть даны 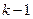раз дифференцируемые функции 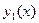, , 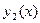…, 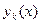. Определителем Вронского этих функций называется следующий определитель 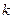-го порядка:

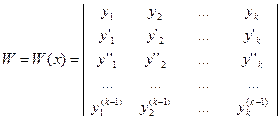
(все функции в этом определителе берутся в некоторой точке ).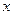

Теорема 1 (первая теорема об определителе Вронского). Пусть функции 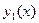, , 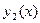…, 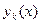линейно зависимы на некотором множестве 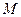. Тогда на этом множестве определитель Вронского тождественно равен 0: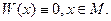

▲ По условию теоремы существуют постоянные 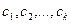, хотя бы одна из которых отлична от 0, такие, что 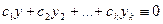. Пусть, например, 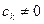. Тогда, разделив это равенство на 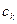и обозначив 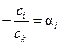, его можно переписать в виде 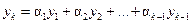. Отсюда 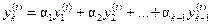, , 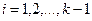и

,

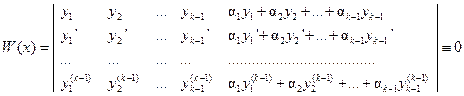так как последний столбец этого определителя является линейной комбинацией остальных его столбцов. ■

Примеры показывают, что теорема, обратная данной, не верна.

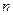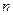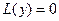
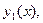
Теорема 2 (вторая теорема об определителе Вронского). Пусть решений линейного однородного дифференциального уравнения -го порядка 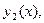…,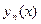линейно независимы на интервале 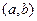. Тогда определитель Вронского этих функций не обращается в 0 ни в одной точке интервала : , .

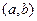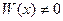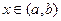Замечание: Первая и вторая теоремы об относятся к разным объектам: первая – к произвольным функциям, а вторая – к решениям линейных однородных дифференциальных уравнений; для последних определитель Вронского либо тождественно равен 0, либо он не обращается в 0 ни в одной точке.

▲ Пусть 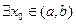: 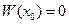. Рассмотрим функцию 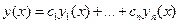. Согласно свойству 3. решений линейного однородного дифференциального уравнения, при любых значениях постоянных 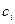, 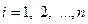функция 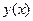является решением уравнения 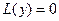. Теперь подберем постоянные 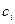так, чтобы эта функция в точке 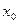удовлетворяла нулевым начальным условиям 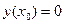, , 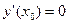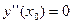… 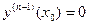. Имеем:

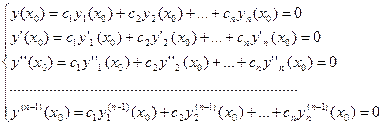(6)

(6) является системой 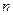линейных однородных уравнений с 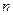неизвестными 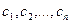. Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных 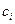, т.е. определитель Вронского 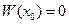. Но тогда система (6), как система 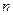линейных однородных уравнений с 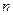неизвестными и определителем, равным 0, имеет ненулевые решения.

Пусть 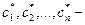одно из таких решений. Тогда функция 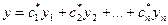удовлетворяет на интервале 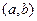уравнению 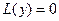и нулевым начальным условиям 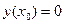, , 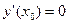…, 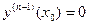. Но этому же уравнению и этим же начальным условиям удовлетворяет и функция 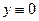. В силу единственности решения задачи Коши, эти два решения должны совпадать:

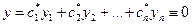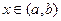, . (7)

Так как в тождестве (7) хотя бы один из коэффициентов 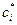отличен от 0, то это тождество означает линейную зависимость на интервале 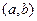функций 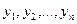, что противоречит условию теоремы. Значит, наше предположение 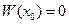не верно. ■