Понижение порядка однородного линейного уравнения

Знание одного частного решения уравнения L[y]=0 позволяет понизить порядок уравнения на единицу.

y₁ – частное решение уравнения L[y]=0.

Введём новую неизвестную функцию U по формуле:

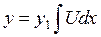(1)

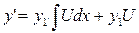(2)

……

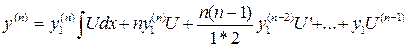
Подставляя формулы (1), (2) в уравнение L[y]=0, получим:

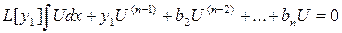(3)

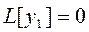
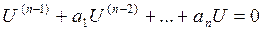(4)

Коэффициенты этого уравнения непрерывны в интервале (a,b), за исключением точек, где у₁ обращается в нуль.

Решая уравнение (4), находим ФСР – U₁, U₂, …, U_n.

Тогда уравнение L[y]=0 имеет решения

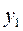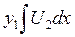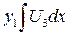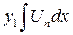, , , …, (5)

Покажем, что решения (5) являются ФСР для уравнения L[y]=0. Предположим, что решения (5) зависимы. Тогда существует соотношение:

a₁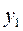+a₂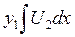+…+ a₃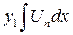=0 (6)

Сокращая на у₁ и дифференцируя, получим:

a₁ U₁ + a₂ U₂ + …+ a_n U_n=0 (7)

что противоречит линейной независимости U₁, U₂, …, U_n.

Если известно k линейно независимых частных решений уравнения L[y]=0, то порядок этого уравнения можно понизить k на единиц.