Исследуем на экстремум функционал
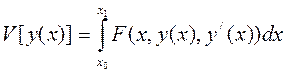 (1)
(1)
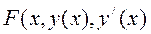 трижды дифференцируема.
трижды дифференцируема.
Предположим, что экстремум функционалом достигается не дважды дифференцируемой кривой 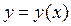 .
.
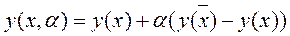 (2)
(2)
при 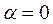 получим кривую
получим кривую 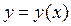 ,
,
при 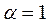 получим кривую
получим кривую 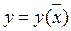 , где
, где 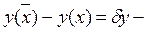 вариация функции
вариация функции 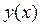 .
.
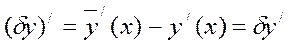 и аналогично
и аналогично
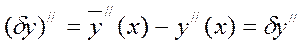 и так далее.
и так далее.
Тогда 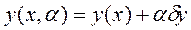 (3) содержит при
(3) содержит при 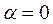 кривую, на которой достигается экстремум, а при
кривую, на которой достигается экстремум, а при 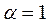 некоторую близкую допустимую кривую.
некоторую близкую допустимую кривую.
Будем рассматривать значение функционала 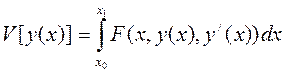 на кривых семейства
на кривых семейства 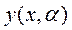
Функционал превращается в функцию от 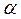 , т.е.
, т.е. 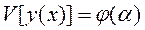 .
.
Эта функция достигает экстремума при 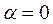 . Необходимое условие этого
. Необходимое условие этого 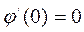 .
.
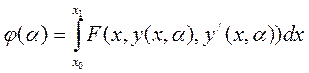 (4)
(4)
Найдём 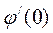 :
:
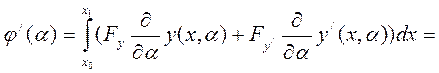
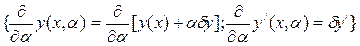
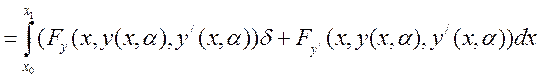
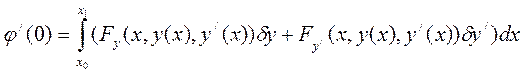 (5)
(5)
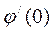 является вариацией функционала и необходимое условие экстремума функционала является условие
является вариацией функционала и необходимое условие экстремума функционала является условие 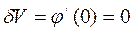 .
.
Итак, 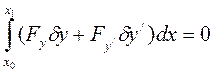 (5/)
(5/)
Интегрируя второе слагаемое по частям, получим:
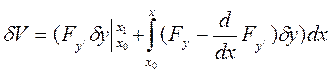 , так как
, так как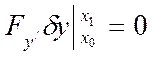
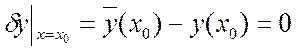 ,
,
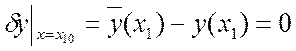 .
.
Все допустимые кривые проходят через фиксированные граничные точки.
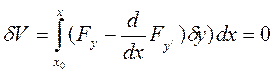 (6)
(6)
Применяя основную лемму вариационного исчисления к интегралу (6), где 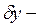 произвольная функция, а
произвольная функция, а 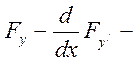 непрерывная функция, получим, что
непрерывная функция, получим, что 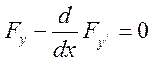 или в развёрнутом виде:
или в развёрнутом виде:
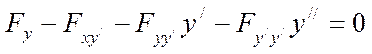 (7)
(7)
Это уравнение называется уравнением Эйлера, а интегральные кривые уравнения Эйлера 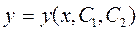 называются экстремалями.
называются экстремалями.
Только на экстремалях может достигаться экстремум функционала 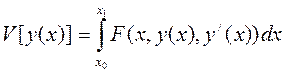 .
.
С1 и С2 находим из условий 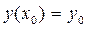 ,
, 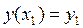 .
.
Это только необходимое условие достижения экстремума.
Замечание:
Краевая задача не всегда имеет решение, или оно не единственно.
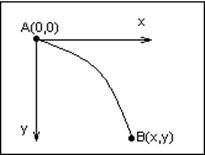
Пример: Задача о брахистохроне.
Определить кривую, соединяющую точки А и В, при движении по которой материальная точка скатится из точки А в точку В в кратчайшее время? (трением и сопротивлением среды пренебречь).
Поместим начало координат в точку А, а ось направим горизонтально, ось 0у – вертикально вниз. Скорость движения материальной точки 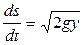 .
.
Тогда 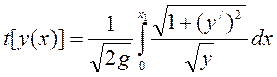 ;
; 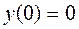 ,
, 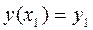 .
.
Уравнение Эйлера для данного функционала имеет вид:
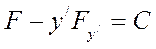 или
или
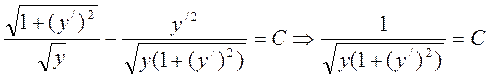
или
|
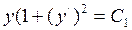 .
.
Введём параметр 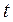 , полагая, что
, полагая, что 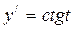 .
.
Тогда 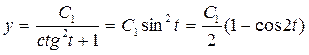 ,
,
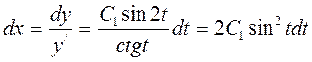 ,
,
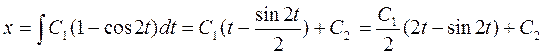 ,
,
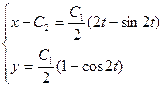
обозначим 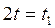 ,
, 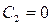 , так как
, так как 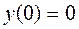 ,
,
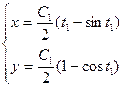 ,
,
где 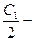 радиус катящегося круга, который определяется из условия прохождения циклоиды через точку
радиус катящегося круга, который определяется из условия прохождения циклоиды через точку 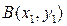 . Брохистохроной является циклоида.
. Брохистохроной является циклоида.
 2014-02-10
2014-02-10 387
387