1) 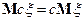
2) 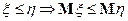
3) 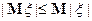
4) Если 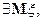 то для любого
то для любого 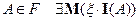 и если
и если 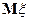 конечно, то
конечно, то 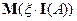 конечно
конечно
5) Если 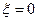
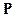 - п.н. (т.е.
- п.н. (т.е. 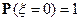 ) то
) то 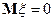
6) Если 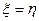
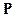 - п.н. и
- п.н. и 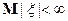 , то
, то 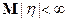 и
и 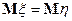
7) Если 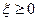 и
и 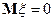 , то
, то 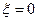
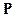 - п.н.
- п.н.
8) Если 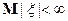 и
и 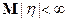 , то
, то 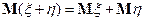
9) Если 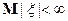 , то
, то 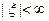
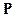 - п.н.
- п.н.
10) Если  и
и 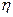 – независимые случайные величины с
– независимые случайные величины с 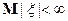 и
и 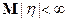 , то
, то 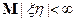 и
и 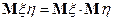
11) Пусть 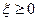
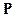 -п.н., тогда для любого
-п.н., тогда для любого 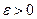 справедливо неравенство Чебышева
справедливо неравенство Чебышева
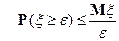
12) Пусть 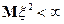 и
и 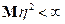 , тогда
, тогда 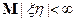 и справедливо неравенство Коши-Буняковского
и справедливо неравенство Коши-Буняковского
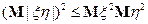
13) Пусть 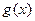 – выпуклая вниз функция и
– выпуклая вниз функция и 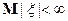 , тогда справедливо неравенство Иенсена
, тогда справедливо неравенство Иенсена
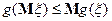
14) Пусть 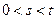 , тогда справедливо неравенство Ляпунова
, тогда справедливо неравенство Ляпунова
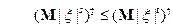
15) 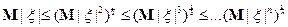
16) Пусть 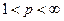 и
и 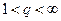 , где
, где 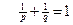 . Если
. Если 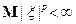 , и
, и 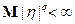 , то
, то 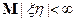 и справедливо неравенство Гельдера
и справедливо неравенство Гельдера
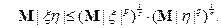
Доказательство свойства 1). 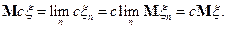
Доказательства свойств 2) - 9) также очевидны.
Доказательство свойства 10). Аппроксимируем
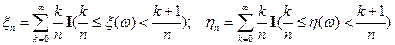
и производим соответствующую замену сумм.
 2014-02-12
2014-02-12 333
333








