2014-02-12
412
Пусть даны две матрицы: А размера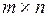 
и В размера 
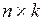. Число элементов строки матрицы А (размерность вектор-строки) равно числу элементов столбца (размерности вектор-столбца) матрицы В, поэтому имеет смысл скалярное произведение этих векторов.
Определение. Произведением матриц А и В называется матрица С, элемент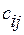 
которой равен скалярному произведению строки 
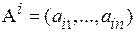матрицы А и столбца 
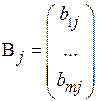матрицы В:
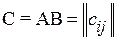, где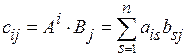 
, (3.5)
; 
.
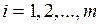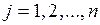Произведение матриц А и В – матрица С – имеет размер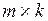 
(
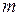– число строк матрицы А, 
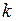– число столбцов матрицы В).
Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скалярные произведения первой строки матрицы А на каждый из столбцов матрицы В; элементы второй строки матрицы С получаются как скалярные произведения второй строки матрицы А на каждый из столбцов матрицы В и так далее. Произведение матриц имеет смысл только в том случае, когда строки первой матрицы и столбцы второй матрицы имеют одинаковое число элементов.
Пример. Пусть даны матрицы
|
|
|
, 
.
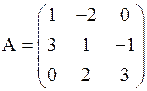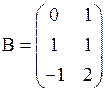Число столбцов матрицы А равно числу строк матрицы В, поэтому произведение матриц АВ имеет смысл. По формулам (3.5) получим: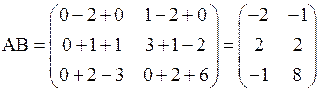 
.
В этом примере произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.
