Ранг матрицы. Определение. Рангом матрицы А размера называется максимальное число линейно независимых векторов в системе

Определение. Рангом матрицы А размера 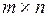называется максимальное число линейно независимых векторов в системе 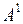,,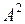…, 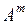ее строк.

Другими словами, рангом матрицы называется такое число 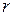, что:

1) среди строк матрицы имеются 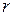линейно независимых;

2) любые (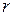+1) строки линейно зависимы.

Максимальное число линейно независимых строк матрицы образуют базис и называются базисными.

Ранг матрицы А обозначают символом r (А).

Теорема 3.1. Ранг совокупности строк матрицы равен рангу совокупности столбцов матрицы.

Из теоремы 3.1 следует, что если матрица А имеет размер ,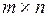
то ранг матрицы не превосходит наименьшего из значени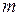й и :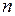

r (А) £ min(, ).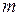

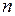Теорема 3.1 утверждает равноправность строк и столбцов матрицы и позволяет нам все последующие свойства ранга матрицы устанавливать лишь для строк и быть уверенными в справедливости их и для столбцов.

Из определения ранга матрицы можно сделать следующие выводы.

1. Если ранг матрицы А равен r, то существует r линейно независимых (базисных) строк матрицы, а остальные (m – r) строк линейно выражаются через указанные r строк.

□ Если r (A)= r, то по определению ранга матрицы среди строк матрицы А найдется r линейно независимых строк. Присоединив любую из остальных (m – r) строк к указанным r строкам, получим систему из 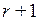строки, которые по определению ранга матрицы должны быть линейно зависимы. Значит, по свойству 6° линейной зависимости векторов (п.1.2) присоединенная строка линейно выражается через указанные r строк. ■

2. Если какие-то r строк матрицы А линейно независимы, а

остальные (m – r) строк линейно выражаются через указанные r строк, то ранг матрицы А равен r.

□ Пусть для определенности линейно независимы первые r строк матрицы А: 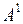,,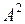…,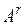– линейно независимы и любая другая строка матрицы линейно через них выражается. Тогда эти r строк образуют базис системы всех строк матрицы А. Рассмотрим любые 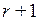строки матрицы А. Если бы они оказались линейно независимыми, то это означало бы, что в системе всех строк матрицы А можно найти базис, состоящий более чем из r векторов, а это невозможно. Значит, любые 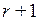строк матрицы А линейно зависимы и ранг матрицы А равен r. ■

Исходя из определения, найдем ранг матрицы в некоторых важных для дальнейшего изложения случаях.

1. Пусть А – нулевая матрица, т.е. А = 0. Тогда матрица А есть совокупность нулевых векторов и по свойству 2° линейной зависимости (п.1.2) такая совокупность линейно зависима, т.е. r (А) = 0.

2. Рассмотрим ступенчатую матрицу вида (3.4):

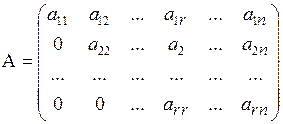, где .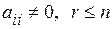

Строки 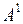,,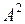…,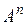матрицы А представляют диагональную систему векторов (1.6), а значит, эта система линейно независима и ранг матрицы А равен числу ее строк, т.е. r (А)= r.

3. Рассмотрим матрицу треугольного вида (3.3). Эта матрица есть частный случай матрицы вида (3.4) при 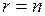, поэтому ранг матрицы треугольного вида равен числу ее строк, т.е. порядку этой матрицы.

4. Рассмотрим диагональную матрицу 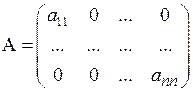, у которой все элементы главной диагонали ненулевые, т.е. 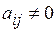при 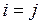. Эта матрица является частным случаем матрицы (3.4). Матрица имеет n линейно независимых строк, поэтому ранг такой матрицы равен ее порядку.

Пример. Найти ранг матрицы .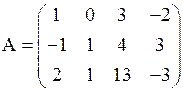

□ Матрица А содержит три вектор-строки: , , .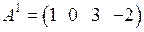

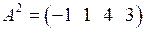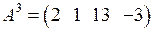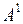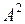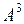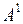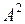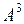Векторы и неколлинеарны, а значит линейно независимы. Вектор является линейной комбинацией векторов и : =3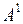+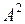, значит векторы 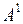,,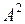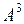линейно зависимы. Максимальное число линейно независимых векторов в системе 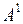,,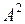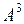строк матрицы А равно 2, следовательно, ранг матрицы А равен 2, r (А)=2. ■