Ортогональная проекция отрезка [AB] прямой на плоскость проекций будет конгруэнтна оригиналу лишь в том случае, когда отрезок параллелен этой плоскости (свойство 6), т.е.
([AB] H)
H) 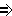 [A1B1]
[A1B1]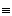 [AB]
[AB]
([CD] V)
V) 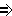 [C2D2]
[C2D2]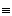 [CD]
[CD]
([EF] W)
W) 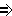 [E3F3]
[E3F3]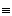 [EF]
[EF]
Во всех остальных случаях отрезок проецируется на плоскость проекции с искажениями. При этом ортогональные проекции отрезка всегда меньше его действительной величины:
|A1B1| < |AB|
|A2B2| < |AB|
|A3B3| < |AB|
Пусть задана система плоскостей V/H и отрезок [AB], заданный своими проекциями. Требуется на эпюре определить его натуральную величину |AB| и углы наклона 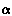 к плоскости H и
к плоскости H и 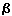 к плоскости V.
к плоскости V.
Угол наклона прямой к плоскости - есть угол между прямой и её проекцией на эту плоскость.
 Рис.6 Рис.6 | [BD] [A2B2] [AC] [A2B2] [AC] [A1B1] [B1B0] [A1B1] [B1B0]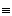 [BC] [A2A0] [BC] [A2A0]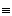 [AD] [AD] 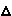 A1B1B0 A1B1B0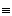 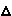 ABC ABC 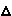 A2B2A0 A2B2A0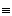 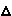 ABD ABD |
Для графического определения на эпюре Монжа действительной (натуральной) величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (фронтальной, профильной) плоскости проекций. Тогда гипотенуза треугольника будет равна натуральной величине отрезка, а угол между гипотенузой и проекцией будет равен углу наклона прямой к этой плоскости.
|
|
|
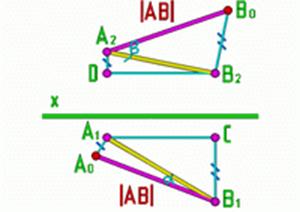 Рис.7 Рис.7 |
Для определения угла наклона прямой к горизонтальной плоскости (угла 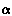 ), построения выполняют на базе горизонтальной проекции.
), построения выполняют на базе горизонтальной проекции.
Для определения угла наклона прямой к фронтальной плоскости (угла 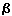 ), построения выполняют на базе фронтальной проекции.
), построения выполняют на базе фронтальной проекции.
 2014-02-12
2014-02-12 858
858








