2014-02-09
1807
Модели
Типы экономического развития и их трендовые
Моделирование одномерных динамических рядов
Траектории, как математические модели экономического развития, классифицируются в зависимости от динамики цепного абсолютного прироста (формулы (4.1) и (4.4)).
Первому типу экономического развития соответствуют траектории с постоянной скоростью (с константным или приблизительно постоянным ростом). Данный тип развития может аппроксимироваться следующими моделями (без учета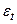 
):
· 
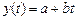– линейной;
· 
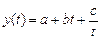– линейно-гиперболической;
· 
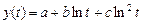– линейно-логарифмической второго порядка.
Второй вид развития может моделироваться траекториями с увеличивающейся скоростью, в частности,
· 
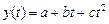– параболической (при 
);
· 
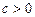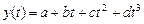– параболой третьего порядка (при 
);
· 
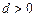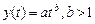– степенной;
· 
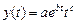– кинетической.
Третий тип развития – это изменение с уменьшающимся ростом. Выделяют следующие подгруппы моделей данного класса:
· уменьшающийся рост, не имеющий предела:
a)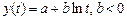 
– линейно-логарифмическая;
b)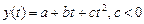 
;
c)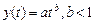 
;
· уменьшающийся рост, имеющий предел:
d)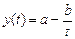 
– гипербола первого порядка;
e)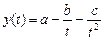 
– гипербола второго порядка.
Особый класс представляют собой модели экономического развития с качественным изменением характеристик. Их особенностью является наличие точки перегиба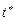 
, в которой скорость меняет свой знак, проходя через нулевое значение абсолютного ускорения (формула (4.6)),
.
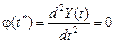Примеры функций данного типа:
· линейно-логарифмическая второго порядка (при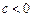 
), для которой
;
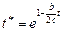· парабола третьего порядка (при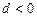 
) с точкой перегиба
.
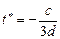Следует указать, что возможна не только кусочная аппроксимация развития на различных участках времени t, но и моделирование всего интервала времени одной функцией (п. 4.4.4).
Методика построения трендовых моделей представляет собой сочетание качественного экономического анализа с формализованными математическими процедурами и реализуется в следующей последовательности.
1. Выбор класса (вида) уравнения тренда исходя из особенностей динамики исследуемого процесса (раздел 4.4.1.).
2. Расчет формальных критериев качества аппроксимации, отражающих степень соответствия модели тренда исходному ряду, а именно, чем меньше значение критерия, тем точнее уравнение (по которому рассчитываются теоретические значения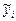 
) моделирует эмпирические данные 
:
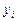· средней квадратичной ошибки аппроксимации (по аналогии с остаточной дисперсией – формула (1.10))
·
,
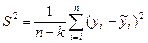где n – длина динамического ряда;
k – количество оцениваемых параметров уравнения тренда;
· относительной (линейной) ошибки аппроксимации
.
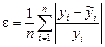3. Статистический анализ случайной компоненты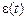 
, которая должна удовлетворять ряду формальных требований (п. 4.4.5).
4. Моделирование сезонных и циклических колебаний в случае установления факта их наличия (п. 4.4.5).
5. Окончательный выбор функции тренда с учетом формальных критериев и характера решаемых задач. Если решаются ретроспективные задачи, то уравнение тренда должно иметь наилучшие значения критериев для всего динамического ряда, если же – перспективные задачи, то предпочтение отдается функции, имеющей минимальные значения ошибок аппроксимаци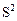и 
и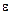 
на последнем (в пределах ретроспективы) интервале оси времени.
