2014-02-12
3263
Идеи методов II этапа:
· перебрать все возможные значения аргумента с проверкой наличия решения;
· поиск корня нелинейной функции заменить поиском корня более простой функции, близкой к исходной;
· уравнение вида f(x)=0 свести к виду g(x)=w(x) и стремиться обеспечить равенство левой и правой частей.
Метод сканирования заключается в разбиении отделенного отрезка на маленькие интервалы, равные заданной точности, с последующим вычислением значения функции на концах этих интервалов. По значениям функции выбирается интервал, где функция меняет знак (или = 0). В качестве решения можно взять любой конец выбранного интервала, но предпочтительнее взять его середину. Уточнение корня можно делать в несколько этапов, уменьшая интервалы разбиения.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА
ДАНО: f(x) – непрерывная функция на [A,B].
[A,B] – отделенный отрезок.
Е – точность вычисления.
НАЙТИ: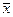 
– приближенное решение.
СВЯЗЬ: n=(B-A)/E – количество интервалов
x0=A, x1=x0+E, …xk+1=xk+E, …xn=B – точки разбиения отрезка
f(x1), f(x2), … f(xn) – значения функции в точках разбиения
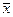=(xk+1 + xk) /2, если f(xk+1)f(xk)<0 (функция меняет знак на отрезке [xk, xk+1 ]
ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).
Метод половинного деления построен на последовательном делении отделенного отрезка пополам и анализе значения функции в этой точке. На каждом следующем шаге выбирается та половина отрезка, на концах которой функция меняет знак. Процесс завершается, когда длина отрезка станет не больше заданной точности или середина отрезка окажется корнем.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА
ДАНО: f(x) – непрерывная функция на [A,B].
[A,B] – отделенный отрезок.
Е – точность вычисления.
НАЙТИ: 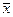– приближенное решение.
СВЯЗЬ: 1) A0=A, B0=B,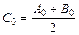
- первое деление отрезка пополам
2) для последующих делений отрезка: к=1,2,...
если функция меняет знак на левой половине, т. е. f(Aк–1)f(Cк–1)< 0, то Вк=Ск-1, Ак=Ак–1
если функция меняет знак на правой половине, т. е f(Bк–1)f(Cк–1)< 0, то Aк=Ск-1, Bк=Bк–1
середина нового отрезка: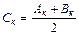 
-
3) 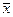=Cк, если | Вк- Ак | ≤E или f (Cк)=0
ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).
Метод хорд заключается в том, что на отделённом отрезке функция заменяется линейной, в качестве которой берётся хорда, стягивающая концы нелинейной функции. Уравнение хорды находится по координатам двух точек. Имея уравнение хорды, можно найти точку пересечения ее с осью абсцисс. Эта точка выбирается в качестве начального приближения к корню. Следующая хорда проводится через точку с координатами
(x0, f(x0)) и закрепленный конец хорды, в качестве которого выбирается один из концов нелинейной функции (в зависимости от поведения функции). Очередным приближением к решению является точка пересечения этой хорды с осью абсцисс. Процесс завершавется, когда модуль разности между соседними приближения станет не больше заданной точности.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА
ДАНО: f(x) – непрерывная функция на [A,B].
[A,B] – отделенный отрезок
Е – точность вычисления.
НАЙТИ: 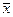– приближенное решение.
СВЯЗЬ: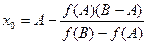 
- начальное приближение к решению (точка пересеченияхорды, стягивающей функцию на отделенном отрезке)
Остальные приближения в зависимости от поведения функции, вычисляются по следующим формулам:
xi+1=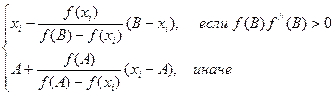
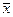= xk+1 , если |xk+1 - xk|£E
ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).
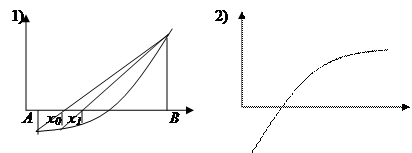
Примечание. Возможны 4 варианта поведения функции, от которого зависит выбор закрепленного конца. В случае 1) закреплен правый конец (f(B)>0 и f″(B)>0, т.к. функция на отрезке выпукла ).
 |
