Решение систем нелинейных уравнений

3) 4)

1)

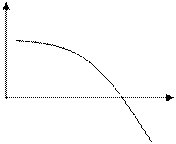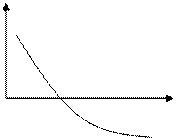
Задание 2.3. В каждом из вариантов определить закрепленный конец.

Вывести формулы x_i+1=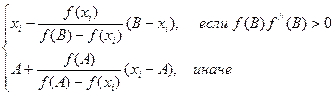

для вычисления последовательных приближений

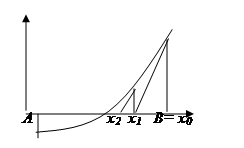
Метод касательных (Ньютона) заключается в том, что на отделённом отрезке функция заменяется линейной, в качестве которой берётся касательная, проводимая к функции в текущей точке последовательности. Уравнение касательной находится по координате одной точки и тангенсу угла наклона (значение производной). В качестве начального приближения берётся левая или правая точка отрезка в зависимости от поведения функции. Имея уравнение касательной, можно найти точку её пересечения с осью абсцисс. Эта точка является следующим приближением к решению. Процесс завершается, когда модуль разности между соседними приближения станет не больше заданной точности.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: f(x) – непрерывная функция на [A,B].

[A,B] – отделенный отрезок.

Е – точность вычисления.

НАЙТИ: 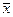– приближенное решение.

СВЯЗЬ:Начальное приближение: x₀=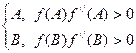

Остальные приближения: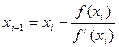

= x_k+1 , если |x_k+1 - x_k|£E

ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).

Задание 2.4. Рассмотреть графически остальные варианты поведения функции. Вывести формулу 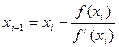для вычисления последовательных приближений.

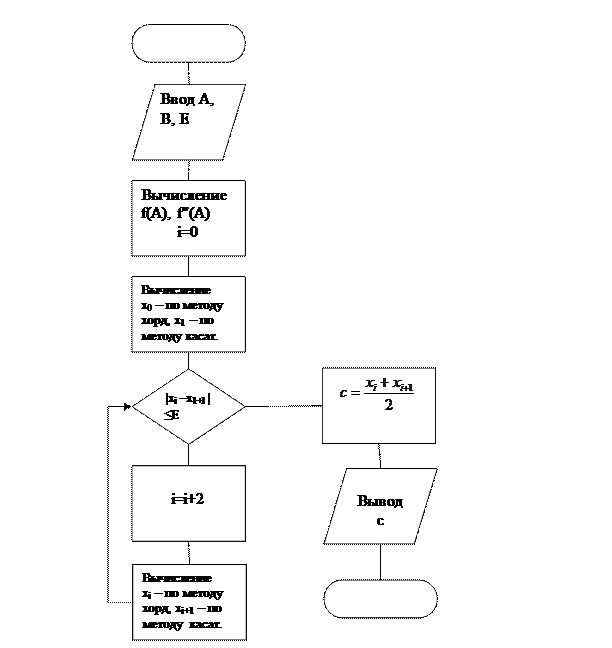
Комбинированный метод заключается в комбинировании метода хорд и метода касательных. На каждом четном шаге решение ищется по методу хорд, а на нечетном – по методу касательных. Процесс завершается, когда модуль разности между соседними приближениями станет не больше заданной точности. В качестве приближенного решения выбирается среднее арифметическое соседних приближений.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: f(x) – непрерывная функция на [A,B].

[A,B] – отделенный отрезок.

Е – точность вычисления.

НАЙТИ: с – приближенное решение.

СВЯЗЬ: 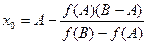x₁=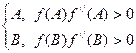

x_2i+2=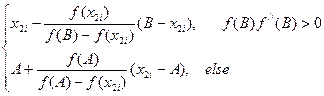

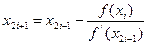
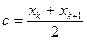, если |x_k+1 - x_k|£E

ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).

АЛГОРИТМ РЕШЕНИЯ.

Метод параболической аппроксимации заключается в том, что на отделённоминтервале исходная функция заменяется параболической. Парабола строится по трём точкам. Коэффициенты параболы определяются из уравнения y = c₂ x² + c₁ x + c₀. На первом этапе точками параболы являются крайние и средняя точка отделённого интервала. В дальнейшем точками для построения параболы является найденный приближённый корень и две предыдущие точки слева и справа от найденного приближения. Процесс завершается, когда модуль разности между соседними приближениями станет не больше заданной точности.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: f(x) – непрерывная функция на [A,B].

[A,B] – отделенный отрезок.

Е – точность вычисления.

НАЙТИ: 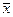– приближенное решение.

СВЯЗЬ: x₀=(В-A)/2, х₁=А; х₂=В – точки, через которые проходит начальная парабола.

Система для нахождения коэффициентов с _i параболы:

c₂ x₀² + c₁ x₀ + c₀,= f(x₀)

c₂ x₁² + c₁ x₁ + c₀,= f(x₁)

c₂ x₂² + c₁ x₂ + c₀,= f(x₂)

Уравнение для нахождения очередного приближения к решению.

c₂ x_k² + c₁ x_k + c₀,= 0

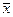= x_k+1 , если |x_k+1 - x_k|£E

ПРИ: f(A)f(B)<0 (признак того, что отрезок [A,B] выбран верно)

Метод простой итерации предполагает предварительное преобразование уравнения f(x)=0 к виду x=φ(x). Затем на отделенном интервале произвольно выбирают начальное значение и подставляют его в правую часть уравнения. Полученное значение рассматривают как очередное приближение к корню. Итерационный процесс продолжается до тех пор, пока модуль разности между соседними приближениями станет не больше заданной точности.

Сходимость итерационного процесса зависит от вида функции φ(x). Приближенное решение будет найдено только, если выполнено условие сходимости: / φ ^/(x)/<1 на отделенном отрезке. В качестве функции φ(x) обычно выбирают φ(x)=х+f(x) или
φ(x)=х-f(x)/k, где 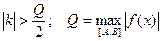и знак k совладает со знаком f ^/(x) на [A,B]

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: φ(x)=х-f(x)/k – непрерывная функция на [A,B]

[A,B] – отделенный отрезок.

Е – точность вычисления.

НАЙТИ: 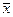– приближенное решение.

СВЯЗЬ: x₀=(В+A)/2 – начальное приближение.

Очередные приближения к решению: x_i+1= φ(x_i)

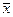= x_k+1 , если |x_k+1 - x_k|£E

ПРИ: f(A)f(B)< 0 (признак того, что отрезок [A,B] выбран верно).

/ φ ^/(x)/≤1 (условие сходимоcти)

ЗАДАЧА 2.3.

Задано уравнение: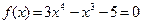

На одном из отделенных отрезков определить закрепленный конец для метода хорд и начертить схематический график.

РЕШЕНИЕ.

При отделении корней в задаче 2.1. получили: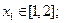

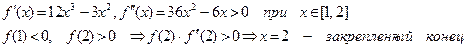
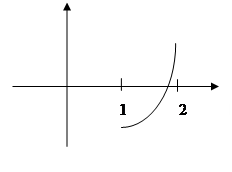f(x) >0 на [1,2], следовательно функция выпукла вниз

ЗАДАЧА 2.4. Задано уравнение: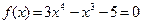

Найти функцию для метода простой итерации.

РЕШЕНИЕ

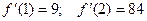
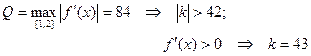
Функция, пригодная для метода итераций, будет иметь вид:

φ(x)=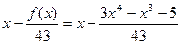

Проверка показывает, что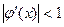

Задание 2.5. На одном из отделенных отрезков определить закрепленный конец для метода хорд и начертить схематический график. Найти функцию для применения метода простой итерации.

1) (x – 2)³ + x + 1 = 0

2) (x + 1)³ – x ² + 2 = 0

ЗАДАЧА 2.5.

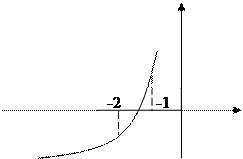
Дано уравнение (x + 3)⁴ – x – 7= 0

1) Определить количество положительных и отрицательных корней и найти область существования корней.

2) Отделить корни графически и аналитически

3) Найти закрепленный конец функции на одном из отделенных отрезков и построить схематический график.

4) Построить функцию для метода итераций

РЕШЕНИЕ

1) Раскроем скобки и приведем подобные члены

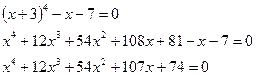
Положительных корней нет, так как нет смены знака коэффициентов при неизвестных.

4 или 2 или 0 отрицательных корней, так как число постоянств знака коэффициентов при неизвестных равно 4.

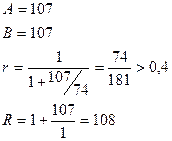
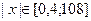
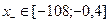
2) Разобьем исходную функцию на две, перенесем в правую часть уравнения и построим графики соответствующих функций

.

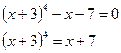По рисунку видно, что графики пересекаются в двух точках, абсцисса которых отрицательна, т.е. исходное уравнение имеет два отрицательных действительных корня, что соответствует предыдущему исследованию. По рисунку определим интервалы, которым принадлежат абсциссы точек пересечения графиков функций:

;

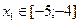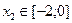
Проверим знак функции на границе области существования и в точках, подозрительных на критические. Определим отделенные отрезки и сузим их.

х	-108	-3	-0,4	-4	-5	-1	-2
Знак у	+	–	+	–	+	+	–

;

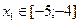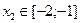
3) Выберем отделенный отрезок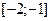

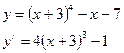
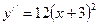
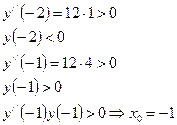
4)

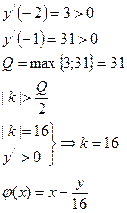
Проверка:

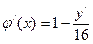
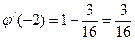
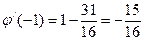
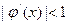. Следовательно, процесс сходится, т.е. функция построена правильно.

Задание 2.6. Сделать полный анализ уравнений

1) 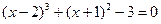2)

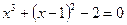
При решении системы уравнений очень сложно отделить корни. Для получения всех возможных решений чаще всего на практике перебирают различные начальные условия поиска.

Метод итераций аналогичен соответствующему методу при решении одного уравнения. Все уравнения системы приводятся к виду:

x₁=f₁(x₁, x₂, …, x_n)

x₂=f₂(x₁, x₂, …, x_n)

…

x_n=f_n(x₁, x₂, …, x_n)

Произвольные начальные значения 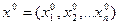подставляются в уравнения системы. Из каждого уравнения системы находятся новые значения 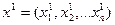и т.д. При выполнении услови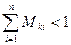й или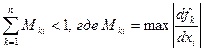

последовательность 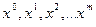сходится к решению

ЗАДАЧА 2.5. Решить систему уравнений

sin(x₁-0,6)-x₂=1,6

3x₁-cos x₂=0,9

E – погрешность вычислений

РЕШЕНИЕ

СВЯЗЬ. Преобразуем систему к виду:

x₂ =sin(x₁-0,6) -1,6= f₂(x₁, x₂)

x₁=(cos x₂)/3+0,3= f₁(x₁, x₂)

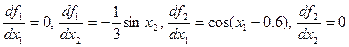
Проверим условие сходимост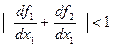и:

и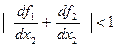

Выберем по графику начальные значения х₁⁰=0,15 и х₂⁰=-2

x₂ⁱ⁺¹ =sin(x₁ⁱ-0,6) -1,6

x₁ⁱ⁺¹=(cos x₂ⁱ)/3+0,3

x₁= x₁ⁱ⁺¹, x₂= x₂ⁱ⁺¹ при /x₁ⁱ⁺¹ –x₁ⁱ/<E, /x₂ⁱ⁺¹ –x₂ⁱ/<E