Закон больших чисел

Под законом больших чисел понимают устойчивость средних: при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности. Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

Теорема 1 (неравенство Маркова). Пусть Х – случайная величина, для которой существует математическое ожидание. Если P (X <0)=0, то

Доказательство.

По условию P (X <0)=0, следовательно, случайная величина Х принимает лишь неотрицательные значения.

1) Пусть Х – дискретная случайная величина. Тогда

P (X ≥1)=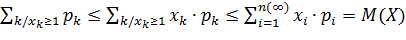

2) Пусть Х – непрерывная случайная величина. Тогда

P (X ≥1)=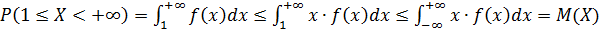

Пример.

Оценить вероятность того, что при 3600 независимых бросаниях игрального кубика число появлений 6 очков будет не меньше 900.

p =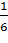, n=3600, M (X)= n∙p =3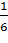600∙=600

P (X ≥900)= P (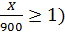

Используем неравенство Маркова и свойство математического ожидания

P (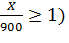≤ M ()=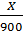

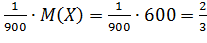
Теорема 2 (неравенство Чебышева). Для любой случайной величины Х, имеющей математическое ожидание М (Х) и дисперсию D (Х), и для любого положительного числа 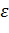справедливо неравенство:

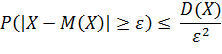Доказательство.

Событие 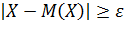равносильно или

По теореме 1 получим: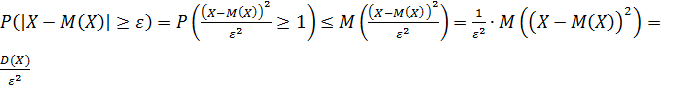

Замечание. Перейдя к противоположному событию, неравенство Чебышева можно записать в виде: .

Пример.

Вероятность появления события А в каждом испытании равна 0,5. Оценить вероятность того, что число появлений события А будет заключено от 40 до 60 в 100 независимых испытаниях.

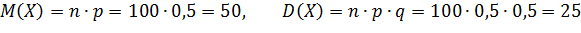
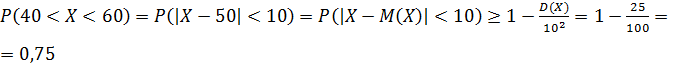
Теорема 3 (теорема Чебышева). Если случайные величины :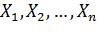

1) попарно независимы;

2) имеют математические ожидания ;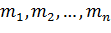

3) имеют дисперсии 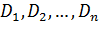, ограниченные в совокупности (то есть для любого k от 1 до n выполняется );

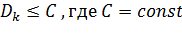то для любого положительного числа 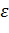выполняется:

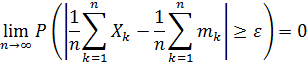
или
.

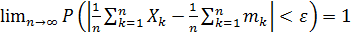Доказательство.

Рассмотрим случайную величину .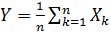

;

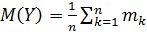Воспользуемся неравенством Чебышева:

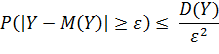
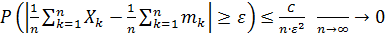(стремится к 0 при )

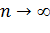или

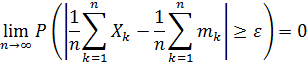
Замечание. Если выполнены условия теоремы Чебышева, то говорят, что при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий:

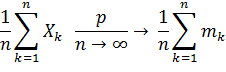
Теорема 4 (теорема Хинчина). Если случайные величины :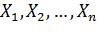

1) попарно независимы;

2) одинаково распределены;

3) имеют математическое ожидание m; то

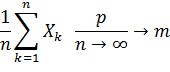
(без доказательства)

Смысл можно пояснить следующим примером. Пусть требуется измерить некоторую величину A. В результате неизбежных ошибок при измерении результат измерения будет случайной величиной. Пусть 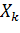- результат k-го измерения. Тогда 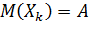и 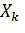- независимые случайные величины. Среднее арифметическое также есть случайная величина, однако с увеличением числа измерений эта величина стабилизируется, приближаясь к A. Этим оправдывается рекомендуемый в практической деятельности способ многократного измерения (семь раз отмерь – один раз отрежь).

Теорема 5 (теорема Бернулли). Частота события A в n независимых испытаниях сходится по вероятности к вероятности наступления события А в одном испытании:

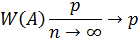
(без доказательства)

Теорема Бернулли обосновывает статистическое определение вероятности.

Рассмотренные теоремы (закон больших чисел) устанавливают факт приближения средних большого числа случайных величин к определенным постоянным. Но этим не ограничиваются закономерности, возникающие в результате суммарного действия случайных величин. Оказывается, что при некоторых условиях совокупное действие случайных величин приводит к нормальному закону распределения.