Порядковая функция орграфа без контуров

Рассмотрим орграф D(V, X), не содержащий контуров, и определим множества

Граф D (V, X) не содержащий контуров – бесконтурный орграф.

Определим для него множества:

V₀ = {u О V | D (u) = Ж};

(*)

V₁ = {u О V \ V₀ | D (u) Н V₀};

V₂ = {u О V \ (V₀ И V₁) | D (u) Н V₀ÈV₁};

…………………………………….

V_r = {u О V \ И V_k | D (u) Н ÈV_k},

Где D(v) – множество образов, r – наименьшее число, такое, что V \ И V_k = Ж (k = 0, 1,…, r).

V₀, V₁, …, V_r – уровни графа.

Уровни образуют разбиение множества вершин V, то есть

И V_k = V (k = 0,1,…,r).

Справедливо утверждение:

Пусть D(V, X) – орграф, r ³ 0, V₀, …, V_r – непустые множества, удовлетворяющие (*), такие, что И V_k = V (k = 0,1,…, r). Тогда D – орграф без контуров.

Функция q (u), определенная на множестве вершин V орграфа без контуров D(V, X) и ставящая в соответствие любой вершине v Î V номер уровня, которому она принадлежит, называется порядковой функцией орграфа D (V, X).

Пример:

Разбить граф D (V, X) на уровни и изобразить в уровневом представлении.

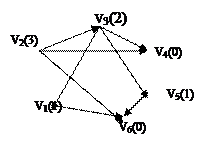
1) Найдём вершины, не имеющие образов и присвоим номер уровня 0:

V₀ = {u Î V | D (u) = Æ} = {u₄, u₆}. Порядковые функции для v₄ и v₆ равны

q (u₄) = 0, q (u₆) = 0.

2) Найдём вершины, образами которых являются u₄ и u₆:

V₁ = {u ÎV \ V₀ | D(u) Н {u₄, u₆}} = {u₁, u₅}. q (u₁) = 1, q (u₅) = 1.

3) V₂ = {u ÎV \ V₀ È D (u) Н {u₄, u₆, u₁, u₅}} = {u₃}, q (u₃) = 2.

4) Тогда V₃ = {u₂}, q (u₂) = 3.

Итак, получили множества V₀, V₁, V₂ и V₃ такие, что их взаимное пересечение пусто, а объединение есть множество вершин V графа. Следовательно граф - без контуров.

Рассмотрим алгоритм выделения уровней орграфа D(V, X) без контуров, использующий задание графа матрицей смежности. Этот алгоритм легко реализуется на ЭВМ:

Шаг 1. Составим матрицу смежности. Образуем под этой матрицей строку l₀, в i – том месте которой укажем число единиц в i – той строке матрицы. Уровень V₀ образуют вершины, которым в строке l₀ соответствует 0. если V = V₀, то задача решена и V₀ – единственный уровень орграфа D. В противном случае переходим к шагу 2.

Шаг 2. Образуем под строкой l₀ строку l₁, ставя под каждым нулем строки символ ´, а на любом другом i – том месте – число единиц в i – ой строке матрицы, не учитывая единицы в столбцах над символами ´ в строке l₁. Уровень V₁ образуют вершины, которым в строке l₁ соответствует число 0. Полагаем j = 1.

Шаг 3. Пусть при некотором j ³ 1уже построены строки l₀ , l₁,…, l_j, по которым получены множества V₀, …, V_j. Если строка l_j состоит из нулей и символов ´, то задача решена и при r = j V₀, …, V_r – уровни орграфа. В противном случае переходим к шагу 4.

Шаг 4. Образуем под строкой l_j строку l_j+1, ставя под каждым нулем и символом ´ символ ´, а на любом другом i – том месте – число единиц в i – ой строке матрицы, не учитывая единицы в столбцах над символами ´ в строке l_j+1. Уровень V_j+1 образуют вершины, которым в строке l_j+1 соответствует число 0. Присваиваем j: = j + 1 и переходим к шагу 3.

Решим предыдущую задачу с помощью матрицы смежности и описанного алгоритма.

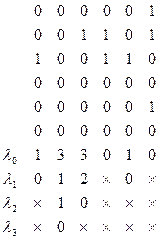
Согласно полученным строкам l_j:

V₀ = {u₄, u₆},

V₁ = {u₁, u₅},

V₂ = {u₃},

V₃ = {u₂}.

Следовательно, для данного графа количество уровней – четыре. Изобразим граф в уровневом представлении:

V₃ V₂ V₁ V₀

Наряду с нахождением уровней орграфа без контуров этот алгоритм позволяет проверить наличие контуров у произвольного графа. Справедливо утверждение:

Орграф D(V, X) содержит хотя бы один контур тогда и только тогда, когда в результате применения алгоритма к графу D появляется строка l_j без нулей.

Такой граф не представим в виде уровней.

Рассмотрим пример. Проверить наличие контуров в орграфе D(V, X), заданном матрицей смежности:

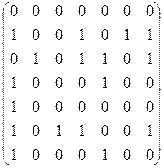
Применяя алгоритм, получим:

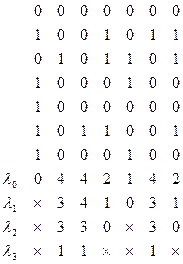
Поскольку в строке l₃ нет нулей, то орграф содержит хотя бы один контур.