Основные понятия и определения. Общий вид обыкновенного дифференциального уравнения первого порядка имеет вид

Лекция 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ

Часть 1. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Общий вид обыкновенного дифференциального уравнения первого порядка имеет вид

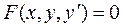, (1.1)

если же это уравнение можно разрешить относительно производной, а именно

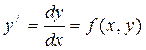, (1.1*)

то тогда уравнение (1.1) будет называться ОДУ разрешенное относительно производной. Функция f(x,y) в уравнении (1.1*) однозначная и непрерывна по совокупности переменных х и у в некоторой области на плоскости (х,у). Эта область называется областью определения уравнения (1.1*).

Если в окрестности точек (х,у) функция f(x,y) обращается в бесконечность, то в этом случае вместо уравнения (1.1*) рассматривается уравнение вида

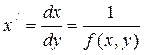. (1.2)

Если правую часть уравнения (1.1) можно представить в виде

,

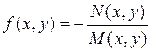тогда уравнение (1.1*) можно записать в форме дифференциалов, а именно

M(x,y)dx + N(x,y)dy = 0. (1.3)

Необходимо отметить, что функции М(x,y), и N(x,y) являются непрерывными функциями в некоторой области изменения переменных x и y. В уравнении (1.3) любую из переменных (х,у), например, х можно принять за функцию, тогда переменной будет аргумент у.

ОДУ (1.1*) и (1.3) равносильны (т.е. имеют одинаковые решения) в области, где M(x,y) ¹0, и, наоборот, при переходе от уравнения (1.3) к (1.1*) и к решениям ОДУ (1.3) необходимо добавлять решения, на которых M(x,y) =0.

Иногда рассматривают ОДУ в так называемой симметрической форме, а именно

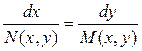. (1.4)

Требование решить уравнения вида (1.1*) и (1.3) соответствует требованию нахождения всех функций вида

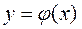, х Î (a,b), (1.5)

обеспечивающих тождество

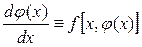, (1.6)

для всех х из интервала (a,b), причем эти функции должны быть определены и непрерывно дифференцируемые в этом интервале.

Решая ОДУ (1.2), находим все функции вида

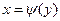, у Î (c,d), (1.7)

которые реализуют тождество

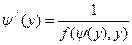(1.8)

для всех у из интервала (c,d).

Для ОДУ первого порядка (1.1*) имеет место теорема, которая гласит о том, что если в уравнении (1.1*) с начальными данными х ₀, у ₀, функция f(x,y) удовлетворяет двум условиям:

1) f(x,y) определена и непрерывна по обеим переменным в некоторой замкнутой области R

R: ½ х – х ₀½£ а, ½ у – у ₀½£ b

где а и в - некоторые положительные числа, а из условия непрерывности функции в замкнутой области следует и то, что она должна быть еще и ограниченной функцией, т.е. должно существовать такое М, что

½ f(x,y) ½£ М, (1.9)

для всех точек области R;

2) f(x,y) в области R удовлетворяет условию Липшица* по переменной у, т.е.

½ f(x,y ₁ ) - f(x,y ₂ ) ½£ L ½ y ₁ - y ₂½, (1.10)

где L – постоянная Липшица, тогда существует единственное решение у (х) уравнения (1.1), удовлетворяющее начальному условию

у (х ₀) = у ₀, (1.11)

определенное и непрерывно дифференцируемое для значений х в интервале (х–х ₀)£ h, где h =min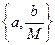, и не выходящее при этих значениях х из области R.

Эта теорема имеет простую геометрическую интерпретацию. Ее можно сформулировать так: если условия теоремы выполнены, то: через каждую точку (х ₀, у ₀) области R проходит кривая, и притом только одна. Такая кривая называется интегральной кривой.

Задача о нахождении решения уравнения (1.1), удовлетворяющего начальному условию (1.11), называется начальной задачей или задачей Коши.

Пусть задана некая функция вида

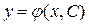, (1.12)

определенная в некоторой области изменения переменных х и С и имеет производную по х. Эта функция будет называться общим решением уравнения (1.1) в области R изменения переменных х и у, если:

1) через каждую точку некой области D изменения переменных x и С проходит интегральная кривая уравнения (1.1), и притом, единственная;

2) для каждой точки (х, у) Î R уравнение (1.12) решается относительно С, так что в результате получается ;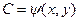

3) функция 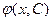из семейства (1.12), отвечающая каждому С, является решением уравнения (1.1).

Если общее решение уравнения (1.1) задано в неявном виде, т.е.

F(x,y,C) = 0, (1.13)

или разрешено относительно произвольной постоянной С

C = φ (x,y,), (1.13^*)

то оно называется общим интегралом этого уравнения.

Решение, в каждой точке которого задача Коши имеет единственное решение, то есть, выполняются условия теоремы существования и единственности решения задачи Коши, называется частным решением. Каждое решение, содержащееся в общем решении, обладает этим свойством, следовательно, является частным решением.

Необходимо отметить, что ОДУ может иметь такое решение, которое не содержится в общем решении, и не является частным решением. Такое решение получило название особого решения, т.к. в каждой его точке нарушается единственность решения задачи Коши, т.е. через каждую его точку проходит не менее двух интегральных кривых. Особое решение не может быть получено из формулы общего решения (1.12) при конкретном числовом значении произвольной постоянной С (но оно может быть получено при С=С(х)). Оно представляет собой особую линию уравнения (1.1). Однако не всякая особая линия является особым решением. Нарушение единственности решения ОДУ происходит в точках, при приближении к которым, 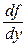неограниченно возрастает, т.е. в точках, в которых 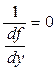. Кривые подозрительные на особые решения, могут быть найдены по уравнению семейства интегральных кривых, заданных или уравнением (1.12) или уравнением (1.13). Если эти уравнения семейства интегральных кривых имеют огибающую, т.е. кривую, обладающую тем свойством по отношению к кривым семейства, что она в каждой своей точке касается, хоть одной кривой семейства интегральных кривых, и вся она состоит из точек касания.

Огибающая семейства интегральных кривых уравнения (1.1) всегда является особым решением этого уравнения.

Кривую подозрительную на огибающую семейства интегральных кривых (1.12), можно найти путем исключения параметра С из системы, составленной из уравнений

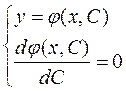(1.14)

Пример 1.1. Проверить является ли для уравнения

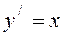(П1.1)

общим решением функция

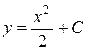. (П1.2)

▲ Проверим, выполняются ли условия, характеризующие функцию (П1.2) как общее решение уравнения (П1.1):

1) через любую точку (х ₀, у ₀) плоскости хOу проходит единственная интегральная кривая уравнения (1.15):

;

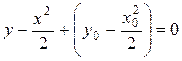2) уравнение (П1.2) решается относительно С для каждой точки (х ₀, у ₀):

;

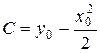3) подставляя полученное значение С, получаем из (П1.2) решение данного уравнения:

.

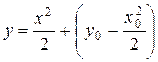Таким образом, мы убедились в том, что (П1.2) есть общее решение уравнения (П1.1). ▲

Пример 1.2. Найти решения уравнения .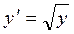

▲ Правая часть этого уравнения 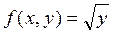определена и непрерывна для всех значений х и у, но частная производная 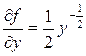обращается в бесконечность при у= 0, т.е. во всех точках оси О х. Для исходного уравнения равенство 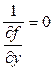имеет вид: 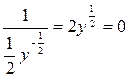или же у= 0. Очевидно, что у= 0 есть решение исходного уравнения, но является ли оно особым? Для этого необходимо проверить, нарушается ли единственность или нет.

Общее решение исходного уравнения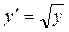можно получить, если привести его к виду: 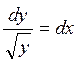. В результате интегрирования этого уравнения получим уравнение семейства интегральных кривых: 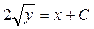или 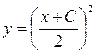. Это уравнение выражает правую «половину» параболы, которая в точке х = - С касается оси О х. Таким образом, через каждую точку оси О х проходит две интегральные кривые: сама ось О х и ветвь параболы. Значит, ось О х (интегральная кривая у =0) есть особое решение для исходного уравнения.

Проверим, является ли интегральная кривая у =0 огибающей семейства интегральных кривых 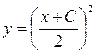. Для этого составим систему (1.14)

.

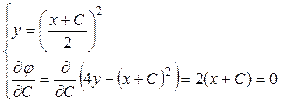Исключая С из этой системы, установим, что кривой, подозрительной на огибающую будет являться ось О х, т.е. у º0. ▲

Пример 1.3. Найти особые решения уравнения:

.

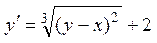▲ Правая часть этого уравнения непрерывна во всей плоскости х О у. Следовательно, единственность может нарушаться лишь за счет нарушения ограниченности частной производной 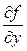. В этом случае 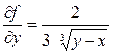, и уравнение 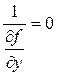имеет вид: 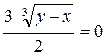или у - х = 0. Определяемая из этого уравнения функция у = х, которая могла бы быть особым решением, не удовлетворяет исходному уравнению, т.к. ее подстановка приводит к соотношению

.

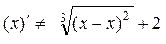Значит, исходное уравнение особых решений не имеет. ▲