Линейное уравнение первого порядка имеет вид:
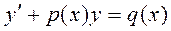 . (2.1)
. (2.1)
Если правая часть этого уравнения q(x) ¹0, то такое уравнение будет называться неоднородным линейным уравнением, а если q(x) =0, то уравнение будет называться однородным линейным уравнением, которое имеет вид:
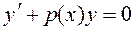 . (2.2)
. (2.2)
В уравнении (2.2) переменные легко разделяются, т.к. его можно записать в виде:
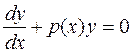 или
или 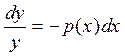 , (2.3)
, (2.3)
откуда можно найти общее решение уравнения (2.3), а именно
 или
или 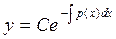 . (2.4)
. (2.4)
Все решения уравнения (2.2) содержатся в формуле (2.4).
Всякое ненулевое решение однородного линейного уравнения (2.2) целиком расположено выше, или ниже оси Ох.
Пример 2.1. Найти общее решение уравнения: 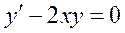 .
.
▲ Разделяя переменные в этом уравнении, будем иметь: 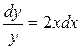 , отсюда получаем:
, отсюда получаем: 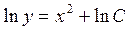 . Следовательно, общее решение исходного уравнения можно записать в виде:
. Следовательно, общее решение исходного уравнения можно записать в виде: 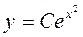 .▲
.▲
Пример 2.2. Через сосуд емкостью а л, наполненный водным раствором некоторой соли, непрерывно протекает жидкость, причем в единицу времени втекает b л воды и вытекает такое же количество раствора. Найти закон изменения содержания соли в сосуде в зависимости от времени протекания жидкости через сосуд.
▲ В данный момент времени t в сосуде содержится х кг соли, следовательно, в каждом литре раствора содержится x/a кг соли, а в b литрах bx/a кг.
Если бы в течение единицы времени, начиная с момента t, концентрация раствора оставалась неизменной, какой она была в момент t, то количество соли в сосуде за эту единицу времени уменьшилось бы на bx/a кг; такова скорость уменьшения количества соли сосуде для момента t.
С другой стороны, производная
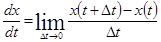
равна скорости прироста количества соли в момент t, поэтому скорость уменьшения количества соли в момент t равна — 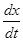 .
.
Итак,
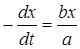 или
или 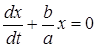 .
.
Полученное уравнение является линейным однородным уравнением относительно функции х. Разделяя в нем переменные, получим
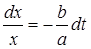
откуда
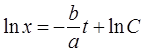
Потенцируя, найдем
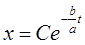 (П2.2.1)
(П2.2.1)
где C — произвольная постоянная.
Предположим, что в некоторый начальный момент t= 0количество соли в сосуде равно A кг.
Полагая в равенстве (П2.2.1) t = 0, найдем
C = A.
Искомый закон изменения содержания соли
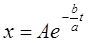 .▲
.▲
Общее решение неоднородного уравнения (2.1) можно найти, используя либо метод Лагранжа, либо метод Бернулли.
1. Метод Лагранжа (метод вариации произвольной постоянной ). Для реализации этого метода необходимо сначала найти решение (2.4) однородного уравнения (2.2), соответствующего неоднородному уравнению (2.1). Затем в общем решении (2.4) произвольную постоянную С представить в виде некоторой дифференцируемой функцией от х: С=С(х), т.е.
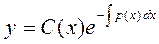 (2.5)
(2.5)
Для нахождения функции С(х) необходимо вычислить производную от (2.5) по х
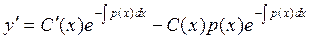 , (2.6)
, (2.6)
а затем саму функцию (2.5) и ее производную (2.6) подставить в уравнение (2.1). В результате получается уравнение:
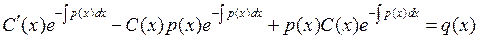
После преобразований приходим к уравнению относительно С¢(х)
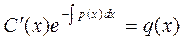 , (2.7)
, (2.7)
откуда, разделяя переменные
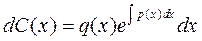 ,
,
и интегрируя полученное уравнение, находим С(х):
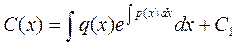 , (2.8)
, (2.8)
где С 1- произвольная постоянная.
Таким образом, подставляя (2.8) в (2.5), получим искомое решение неоднородного линейного уравнения (2.1):
 . (2.9)
. (2.9)
Эта формула называется формулой Эйлера и в ней содержатся все решения уравнения (2.1).
Пример 2.3. Найти решение неоднородного уравнения: 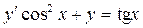 , при начальном условии у (0)=0.
, при начальном условии у (0)=0.
▲ Для нахождения общего решения воспользуемся методом Лагранжа. Для этого составим однородное уравнение, соответствующее исходному неоднородному уравнению, а именно: 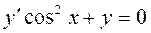 , и, разделив переменные:
, и, разделив переменные: 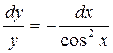 , найдем его общее решение
, найдем его общее решение 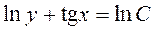 или
или 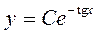 . Затем представим в этом уравнении произвольную постоянную С как функцию от х:
. Затем представим в этом уравнении произвольную постоянную С как функцию от х:
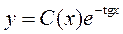 . (П2.3.1)
. (П2.3.1)
Для того, чтобы определить С(х) вычислим производную от (П2.3.1)
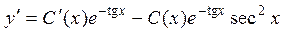 . (П2.3.2)
. (П2.3.2)
Далее, подставив (П2.3.1) и (П2.3.2) в исходное уравнение, придем к уравнению
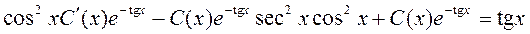 ,
,
или
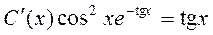 .
.
Откуда находим:
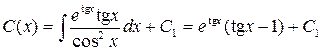 .
.
Таким образом, получаем общее решение исходного неоднородного уравнения:
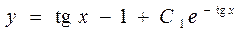 . (П2.3.3)
. (П2.3.3)
Используя начальное условие у (0)=0, можно получить решение задачи Коши и выделить из всей совокупности решений (П2.3.3) частное решение, соответствующее этому условию: 0=-1+ С, откуда С = 1. Следовательно, частное решение будет иметь вид
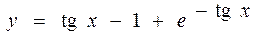 .▲
.▲
2. Метод Бернулли. По этому методу общее решение неоднородного уравнения (1.38) ищется в виде
y=uv, (2.10)
где – u и v новые неизвестные дифференцируемые функции переменной х.
Подставив функцию (2.10), а также ее производную
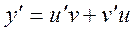
в уравнение (2.1), получим
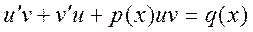 . (2.11)
. (2.11)
Приравнивая сумму второго и третьего слагаемых этого уравнения нулю
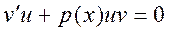 , (2.12)
, (2.12)
из уравнения (2.11) получим
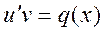 (2.13)
(2.13)
В уравнении (2.12), предполагая, что u ≠ 0 (при u = 0 решение уравнения (2.1) будет равно нулю, т.к. y=uv), можно сократить на u. Тогда получим линейное однородное уравнение относительно неизвестной функции v
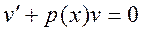 ,
,
решение которого дается формулой (2.4)
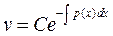 . (2.14)
. (2.14)
Подставляя эту функцию в уравнение (2.13), прировняв С =1 (для нахождения функции u достаточно только одной функции v), получим
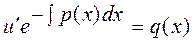 .
.
Разделяя переменные в этом уравнении
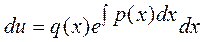
и интегрируя его, найдем функцию u
 . (2.15)
. (2.15)
Таким образом, подставляя найденные функции (2.14) и (2.15) в (2.10), получим формулу Эйлера (2.9)
 .
.
Пример 2.4. Используя метод Бернулли найти общее решение уравнения:
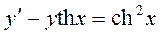 . (П2.4.1)
. (П2.4.1)
▲ Следуя методу Бернулли, решение будем искать в виде:
y = uv. (П2.4.2)
Подставив у, определяемое уравнением (П2.4.2), и вычисленную ее производную: 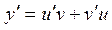 , в уравнение (П2.4.1), придем к уравнению:
, в уравнение (П2.4.1), придем к уравнению:
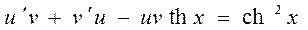 ,
,
или
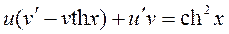 .
.
Составим уравнение (2.12) 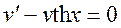 и решим его относительно v:
и решим его относительно v: 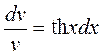 . Интегрируя далее, получим:
. Интегрируя далее, получим:
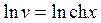 ,
,
или
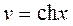 (П2.4.3)
(П2.4.3)
(постоянную интегрирования не вводим, т.к. достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для определения u составим уравнение (2.13):
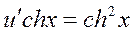 ,
,
откуда находим
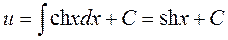 . (П2.4.4)
. (П2.4.4)
Подставляя (П2.4.3) и (П2.4.4) в (П2.4.2), найдем общее решение исходного уравнения:
 .▲
.▲
Пример 2.5. Найти решение уравнения: 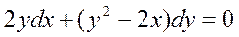 .
.
▲ Это уравнение не является линейным относительно функции у. Однако, если разделить это уравнение на 2 ydy, то оно приводится к линейному, но уже с неизвестной функцией х: 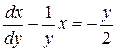 . Используя сразу формулу общего решения (2.9), получим:
. Используя сразу формулу общего решения (2.9), получим:
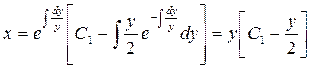 .▲
.▲
Пример 2.6. Рассмотрим вентиляцию забоя объемом V (м3), в котором в процессе проведения работ накапливаются вредные газообразные выделения в количестве Z в час. Пусть обмен воздуха в течении 1 часа составляет М (м3/ч), причем приточный воздух содержит вредные вещества в концентрации m на 1 м3. Требуется найти концентрацию Z (на 1 м3) вредных выделений в забое через время t после начала работы, если начальное значение этой концентрации (остаток загрязнений от предыдущей смены) составляет Z 0.
▲ За малый промежуток времени dt концентрация вредных выделений Z увеличивается на dZ. Следовательно общее количество выделений составит VdZ и оно будет состоять из выделений, принесенных приточным воздухом - mМdt, и выделений образовавшихся в процессе работы - Zdt за вычетом количества вредных выделений, которое содержалось в извлеченном из забоя за время dt воздухе. Предположим, что за малый промежуток времени dt изменение концентрации вредных выделений равно – ZМdt. Следовательно, уравнение вентиляции забоя имеет вид:
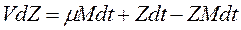 или
или 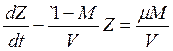
Полученное уравнение является линейным неоднородным уравнением, которое будем решать, используя сразу формулу общего решения (2.9):
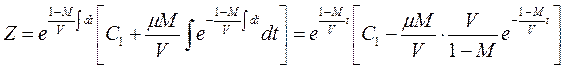
или
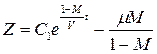 .
.
Удовлетворяя начальному условию 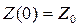 , определим значение произвольной постоянной
, определим значение произвольной постоянной 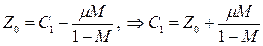 . Таким образом, окончательное решение исходной задачи имеет вид:
. Таким образом, окончательное решение исходной задачи имеет вид:
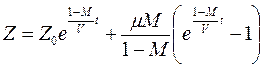 .▲
.▲
Пример 2.7. Установить закон изменения концентрации утяжелителя в суспензии по времени при постоянном его добавлении в суспензию.
▲ Если количество утяжелителя в суспензии q, аего концентрация — q / V = ξ, где V — объем распространения в суспензии, то вводимый утяжелитель определяется в количестве, пропорциональном его наличному содержанию в суспензии. С другой стороны, концентрация утяжелителя повышается в результате постоянного его добавления.
В итоге этих двух взаимосвязанных процессов находим, что изменение концентрации утяжелителя в суспензии по времени можно описать следующим дифференциальным уравнением
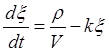 (П2.7. 1)
(П2.7. 1)
где k — постоянная скорость добавления, ρ — количество добавляемого утяжелителя, мг/мин.
Если утяжелитель не прибавляется, то ρ = 0 и уравнение (П2.7. 1) сводится к равенству
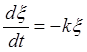
тогда как при отсутствии вливания k = Q и уравнение (П2.7. 1) примет вид
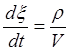
Представляя уравнение (П2.7. 1) в виде
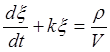 (П2.7. 2)
(П2.7. 2)
замечаем, что уравнение (П2.7. 2) представляет собой неоднородное линейное уравнение, решить которое можно, используя либо метод Лагранжа (метод вариации произвольной постоянной), либо метод Бернулли. Рассмотрим метод Лагранжа. Для этого составим для уравнения (П2.7. 2) соответствующее однородное уравнение
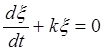
И найдем его решение, разделив в нем переменные
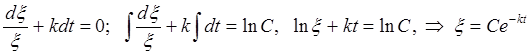
Будем варьировать постоянную С, т.е. представим ее как функцию t, С=С(t). Тогда решение неоднородного уравнения (П2.7. 1) можно представить в виде
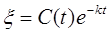 (П2.7. 3)
(П2.7. 3)
Вычислим от (П2.7. 3) производную по (t) и подставим ее, а также функцию (П2.7. 3) в уравнение (П2.7. 2)
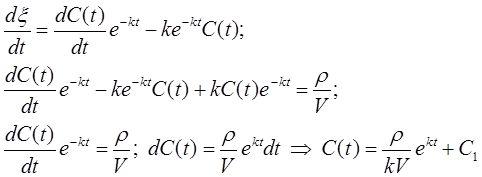
Подставив найденную функцию С=С(t) в решение (П2.7. 3), получим окончательный вид решения уравнения (П2.7. 2)

Используя начальные условия, по которым при t =0 ξ = 0, получим
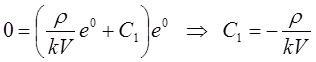 .
.
Таким образом, решение задачи Коши будет иметь вид
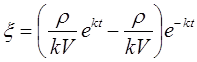
или концентрация утяжелителя в любой момент времени определяется по формуле
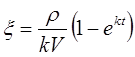 . ▲
. ▲
Пример 2.8. При размыкании цепи (в момент появления искры) сопротивление цепи R быстро возрастает от первоначальной величины R oдо бесконечности. На основании опыта допускают, что зависимость R от t в этом процессе выражается
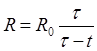
где τ — время всего процесса размыкания. Найти силу тока i в любой момент в цепи при постоянной электродвижущей силе Е и самоиндукции L.
▲ Так как в цепи действуют электродвижущая сила источника Е и электродвижущая сила самоиндукции 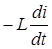 ,то результирующая электродвижущая сила
,то результирующая электродвижущая сила
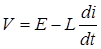 .
.
По закону Ома
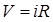 или
или 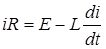 ,
,
В процессе размыкания цепи 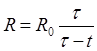 .Отсюда получаем дифференциальное уравнение процесса
.Отсюда получаем дифференциальное уравнение процесса
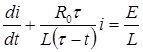 , (П2.8. 1)
, (П2.8. 1)
которое является линейным неоднородным уравнением.
Общее решение уравнения (П2.8.1) в соответствии с формулой Эйлера можно представить в виде
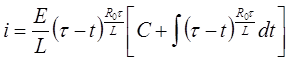 .
.
Возможны два случая: 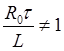 и
и 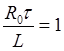 .
.
В первом случае после раскрытия интеграла в квадратных скобках общее решение будет
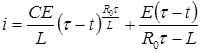 . (П2.8.2)
. (П2.8.2)
Во втором случае общее решение примет вид
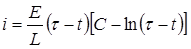 . (П2.8.3)
. (П2.8.3)
Начальное условие: в момент начала размыкания при t = 0 сила тока 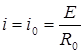 . Тогда в первом случае
. Тогда в первом случае
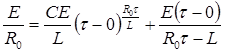
откуда
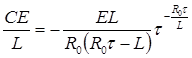 (П2.8.4)
(П2.8.4)
Выражение (П2.8.4) подставляем в общее решение (П2.8.2) и получаем
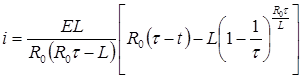 .
.
Аналогично во втором случае
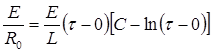
Откуда
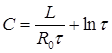
или, так как 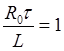 , то
, то
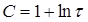 (П2.8.5)
(П2.8.5)
Подставляя выражение (П2.8.5) в общее решение (П2.8.3), получим формулу для расчета силы тока i в момент появления искры при размыкании цепи в любой момент при постоянной электродвижущей силе Е и самоиндукции L
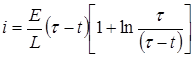 .▲
.▲
Пример 2.9. Найти закон нагрева теплообменника при постоянном притоке теплоты.
▲ Пусть: dT — изменение температуры отопительного аппарата в течение времени dt; G — вес аппарата; с — специфическая теплота материала аппарата; λ — коэффициент теплопереноса поверхностью аппарата (на единицу площади для повышения температуры на 1°С); Q — количество поступающей теплоты в единицу времени; S — поверхность теплопередачи аппарата; T 1— наружная температура; Т — T 1— превышение наружной температуры теплообменника.
В течение времени dt происходят следующие процессы:
а) в теплообменник поступает количество теплоты, равное Qdt;
б) в аппарате накапливается количество теплоты, равное GcdT;
в) отдается в окружающую среду количество теплоты, равное S(Т — T 1 )λt.
Суммируя эти количества, получаем уравнение теплового баланса

или
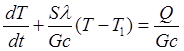
Полагая 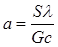 и
и 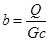 , дифференциальное уравнение процесса запишем в виде линейного неоднородного уравнения:
, дифференциальное уравнение процесса запишем в виде линейного неоднородного уравнения:
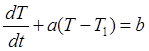 (П2.9.1)
(П2.9.1)
Для нахождения решения уравнения (П2.9.1) воспользуемся формулой Эйлера
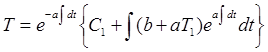
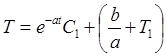 (П2.9.2)
(П2.9.2)
Используя начальное условие: при t = 0 T=T 1, найдем чему равна произвольная постоянная
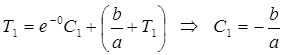
Тогда уравнение процесса принимает вид
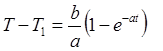 (П2.9.3)
(П2.9.3)
или, подставляя значения а и b, получим:
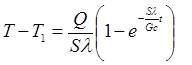
При T 1 = 0из уравнения (П2.9.3) получим
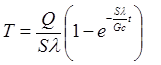
или
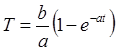 (П2.9.4)
(П2.9.4)
Исследуем этот закон. При t→∞ получаем
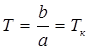
где Т к — конечная температура теплообменника. Уравнение (П2.9.4) может быть записано в виде
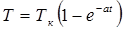 (П2.9.5)
(П2.9.5)
Подставляя теперь в уравнение (П2.9.5) значение
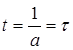
Получаем
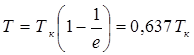
Время τ — называется постоянной времени. ▲
Рассмотрим уравнение вида
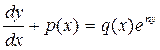 . (2.16)
. (2.16)
приводится к линейному уравнению с помощью подстановки
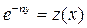 . (2.17)
. (2.17)
Тогда после дифференцирования (2.17), получим
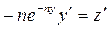 . (2.18)
. (2.18)
После подстановки (2.17) и (2.18) в (2.16) придем к неоднородному линейному уравнению относительно новой функции z:
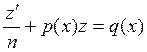 (n ¹0). (2.19)
(n ¹0). (2.19)
Пример 2.10. Записать общий интеграл уравнения: 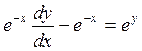 .
.
▲ Умножив обе части исходного уравнения на ех, получим уравнение вида (2.16)
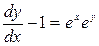 .
.
Следовательно, можно применить подстановку (2.17): 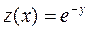 . Тогда получим последовательно
. Тогда получим последовательно
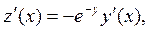
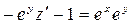 ,
,  .
.
Полученное уравнение линейно относительно z. Его решение можно получить, используя формулу (2.9):
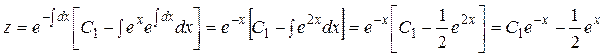
Осталось перейти к искомой функции и записать общий интеграл исходного уравнения:
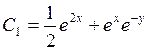 .▲
.▲
Пример 2.11. Найти общее решение уравнения:
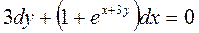 .
.
▲ Это уравнение можно привести к виду:
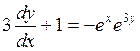 .
.
Это уравнение относится к уравнениям вида (2.16). Поэтому можно воспользоваться подстановкой (2.17): 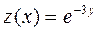 . Тогда последовательно получим
. Тогда последовательно получим
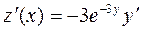 ,
, 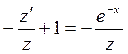 ,
, 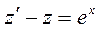 .
.
Общее решение этого уравнения находим по формуле (2.9)
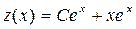 .
.
Следовательно, общее решение исходного уравнения будет иметь вид:
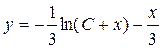 .▲
.▲
Рассмотрим уравнение вида
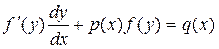 . (2.20)
. (2.20)
Это уравнение приводится к линейному уравнению, если ввести новую функцию
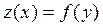 , (2.22)
, (2.22)
тогда получим последовательно
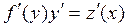
и
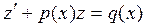 . (2.23)
. (2.23)
Уравнение (2.23) представляет собой линейное уравнение относительно функции z.
Пример 2.12. Найти общее решение уравнения:
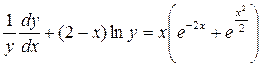 .
.
▲В этом уравнении коэффициент при 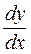 представляет собой производную от коэффициента при (2- х), следовательно, исходное уравнение относится к уравнениям вида (2.20), поэтому, применив подстановку (2.23):
представляет собой производную от коэффициента при (2- х), следовательно, исходное уравнение относится к уравнениям вида (2.20), поэтому, применив подстановку (2.23): 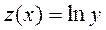 , получим
, получим

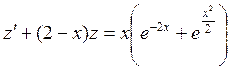 .
.
Последнее уравнение является линейным относительно z. Применив формулу (2.9), получим
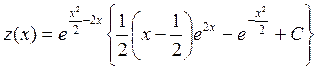 .
.
Следовательно, общее решение исходного уравнения будет иметь вид:
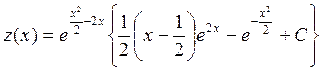 .▲
.▲
Рассмотрим уравнение вида
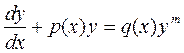 . (2.24)
. (2.24)
Если в этом уравнении степень искомой функции, находящейся в правой части неравна нулю и единице, то есть 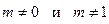 , то уравнение (2.24) будет называться уравнением Бернулли, которое приводится к линейному уравнению с помощью замены
, то уравнение (2.24) будет называться уравнением Бернулли, которое приводится к линейному уравнению с помощью замены
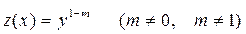 . (2.25)
. (2.25)
Вычислив производную от функции (2.25) по х
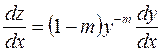 ,
,
и подставив ее в уравнение (2.24), а затем, разделив на 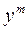 , получим
, получим
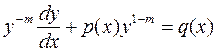
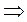
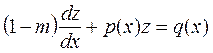
или
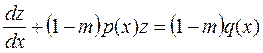 . (2.26)
. (2.26)
Полученное уравнение (2.26) является линейным неоднородным уравнением
Пример 2.13. Найти решения уравнения:
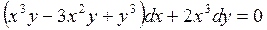 .
.
▲ Разделив обе части исходного уравнения на dx ¹0 (x =0 – очевидное решение), получим уравнение Бернулли
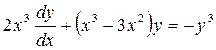 .
.
Считая у¹ 0 (у =0 – тривиальное решение), делим обе части последнего уравнения на (- у 3) и делаем замену 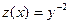 . Тогда получим
. Тогда получим
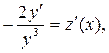
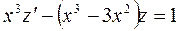 .
.
Решая это уравнение, находим
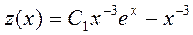 .
.
Теперь запишем все решения исходного уравнения
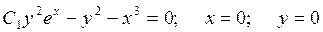 .▲
.▲
Рассмотрим уравнение вида
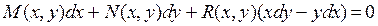 . (2.27)
. (2.27)
Если в этом уравнении M и N – однородные функции степени m, а R – однородная функция степени n (n¹m- 1), то уравнение (2.27) называют уравнением Дарбу-Миндинга. При этом одна из функций M и N может быть тождественным нулем.
Уравнение (2.27), в котором N ¹0, при помощи замены
y=zx, (2.28)
где z - новая неизвестная функция.
Заменой (2.28) уравнение (2.7) приводится к уравнению Бернулли (2.24) с искомой функцией х от независимой переменной z, а затем по описанному выше способу приводится к линейному уравнению.
Если Nº 0, то заменой (2.28) приводит уравнение (2.27) к уравнению с разделяющимися переменными. Полупрямые 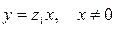 , где zi – корни уравнения
, где zi – корни уравнения 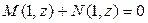 , могут быть особыми.
, могут быть особыми.
Пример 2.14. Найти общий интеграл уравнения:
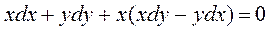 .
.
▲ Полагая y=zx и вычислив dy=xdz+zdx, получим
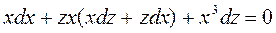 ,
,
или
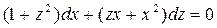 .
.
Отсюда получаем уравнение
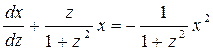 ,
,
которое является уравнением Бернулли относительно функции х и независимой переменной z. Интегрируя это уравнение, как было указано в примере 2.13, получим
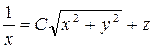 .
.
Заменяя z на у/х, получим общий интеграл исходного уравнения
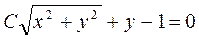 .▲
.▲
Пример 2.15. Найти все решения уравнения:
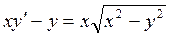 .
.
▲ Это уравнение типа (2.27)
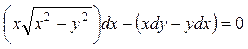 ,
,
в котором N =0. Полагая y=zx и dy=xdz+zdx, получим: 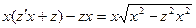 или
или 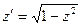 . Интегрируя это уравнение, находим
. Интегрируя это уравнение, находим
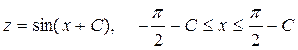 ,
,
z= ±1 – особые решения. Следовательно,
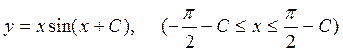
y= ± х, х ¹0 – особые решения.
Необходимо заметить, что все интегральные кривые примыкают к началу координат. Они расположены между полупрямыми y= ± х, х ¹0 (в углах, заключающих ось Ох), которые, образуя границу области задания исходного уравнения, сами являются решениями этого уравнения. Эти решения суть огибающие семейства интегральных кривых, составляющих общее решение. ▲
Рассмотрим уравнение вида
 , (2.29)
, (2.29)
правая часть которого представляет собой квадратный трехчлен искомой функции у. Такое уравнение называется уравнением Риккати.
Отметим, что при а(х) =0 уравнение (2.29) является линейным уравнением, а при с(х) =0 уравнение (2.29) становится уравнением Бернулли с т =2, поэтому, называя уравнение вида (2.29) уравнением Риккати, всегда предполагают а(х) ¹0 и с(х) ¹0.
Если коэффициенты а(х), b(х) и с(х) непрерывны на некотором промежутке и правая часть уравнения (2.29) удовлетворяет условиям теоремы существования и единственности решения задачи Коши, то тогда уравнение Риккати не имеет особых решений и задача Коши для него
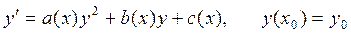 (2.30)
(2.30)
имеет единственное решение при любых условиях.
Для нахождения общего решения уравнения Риккати (2.30) необходимо знать хотя бы одно его частное решение. В этом случае оно приводится к линейному уравнению с помощью замены
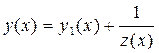 , (2.31)
, (2.31)
где y 1(x)- известное частное решение уравнения (2.30), а z (x) – новая неизвестная функция.
Частное решение уравнения Риккати можно легко подобрать если:
1. 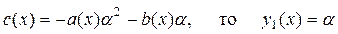 .
.
2.  то
то 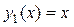 .
.
Если уравнение (2.30) имеет вид
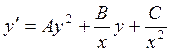 , (2.32)
, (2.32)
где А,В,С – постоянные числа, причем (В +1)2 ³ 4 АС, то такое уравнение имеет частное решение вида
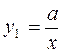 , (2.33)
, (2.33)
где а – некоторое постоянное число, определяемое подстановкой (2.33) в уравнение (2.32).
Уравнение (2.32) является также обобщенным однородным уравнением, в котором k=- 1, и, следовательно, подстановкой y=z/x всегда приводится к уравнению с разделяющимися переменными.
Уравнение Риккати вида
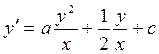 или
или 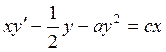 (2.34)
(2.34)
подстановкой
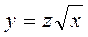 (2.35)
(2.35)
приводится к уравнению с разделяющимися переменными
 ,
,
и, следовательно, всегда интегрируется в элементарных функциях.
Необходимо отметить, что если в уравнении (2.30) а(х)=а=const, b(x)=0, c(x)=cxm, где а,с,т – постоянные, то такое уравнение принимает вид
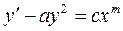 , (2.36)
, (2.36)
и называется специальным уравнением Риккати.
Если в уравнении (2.36) т =0, то это уравнение с разделяющимися переменными. При т = -2 уравнение (1.70) приводится к уравнению с разделяющимися переменными с помощью подстановки y=z/x.
Специальное уравнение Риккати (2.36) интегрируется в элементарных функциях при любом т, для которого выражение 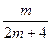 является целым числом, т.е. для
является целым числом, т.е. для
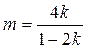 , (2.37)
, (2.37)
где k – целое или ¥.
А) Если равенство (2.37) выполняется при k >0, то в уравнении (2.36) делаем замену 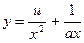 , приводящую уравнение (2.36) к виду
, приводящую уравнение (2.36) к виду 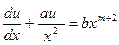 . Полагая далее
. Полагая далее 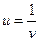 , имеем
, имеем 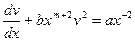 . Наконец после замены
. Наконец после замены 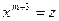 приходим к уравнению
приходим к уравнению 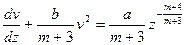 . Такие преобразования проводим до тех пор, пока не получим уравнение с разделяющимися переменными.
. Такие преобразования проводим до тех пор, пока не получим уравнение с разделяющимися переменными.
Если равенство (2.37) выполняется при k <0, то указанные преобразования следует проводить в обратном порядке.
При всех других т уравнение (2.36) не интегрируется.
Пример 2.16. Найти общее решение уравнения:
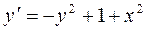 .
.
▲ Это уравнение является уравнением Риккати, в котором а(х) =- 1, b(x)= 0 и с(х) = 1 +х2. Проверка условия 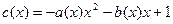 . Привело к результату: 1 +х2= 1 + х2. Следовательно, это условие выполняется и за частное решение исходного уравнения можно принять функцию:
. Привело к результату: 1 +х2= 1 + х2. Следовательно, это условие выполняется и за частное решение исходного уравнения можно принять функцию: 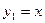 . Таким образом, полагая
. Таким образом, полагая 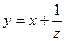 и вычислив
и вычислив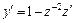 , приводим исходное уравнение к неоднородному линейному уравнению:
, приводим исходное уравнение к неоднородному линейному уравнению: 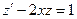 . Откуда
. Откуда
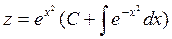 .
.
Следовательно, общее решение исходного уравнения Риккати имеет вид:
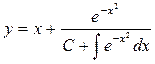 .▲
.▲
Пример 2.17. Решить задачу Коши для уравнения Риккати:
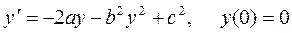 .
.
где a,b,c – постоянные отличные от нуля числа.
▲Так как в исходном уравнении a,b,c – постоянные числа, то оно является уравнением с разделяющимися переменными. Разделяем переменные: 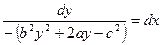 и интегрируя, получаем
и интегрируя, получаем 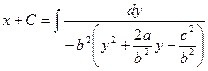 .
.
Преобразуем интеграл, выделяя полный квадрат трехчлена
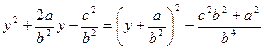
и вводя обозначения 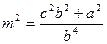 ,:
,:
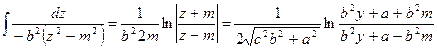 .
.
Обозначив 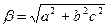 , запишем решение:
, запишем решение:
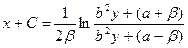 .
.
Далее потенцируем
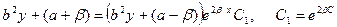
и выражаем у:
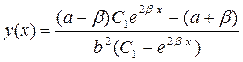 .
.
Поделив числитель и знаменатель на 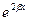 , получим общее решение рассматриваемого уравнения Риккати:
, получим общее решение рассматриваемого уравнения Риккати:
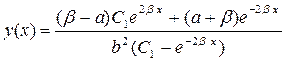 .
.
Используя начальное условие у(0)=0, находим: 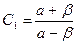 , и подставляем его в общее решение. В результате получаем решение поставленной задачи Коши:
, и подставляем его в общее решение. В результате получаем решение поставленной задачи Коши:
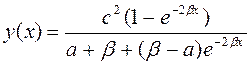 .▲
.▲
Пример 2.18. Путем подбора частного решения решить уравнение:
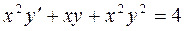 .
.
▲ Это уравнение является уравнением Риккати вида (2.32): 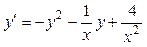 , где A=- 1, B =-1 и C =4. Поскольку для этого уравнения выполняется неравенство (В +1)2 ³ 4 АС, то частное решение исходного уравнения ищем в виде
, где A=- 1, B =-1 и C =4. Поскольку для этого уравнения выполняется неравенство (В +1)2 ³ 4 АС, то частное решение исходного уравнения ищем в виде 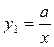 , где a=const. Подставив его в исходное уравнение, получим:
, где a=const. Подставив его в исходное уравнение, получим: 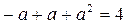 , откуда а =±2.
, откуда а =±2.
Пусть а = 2. Тогда частное решение у 1 равно: 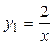 . Следовательно, подстановка (2.33) принимает вид:
. Следовательно, подстановка (2.33) принимает вид: 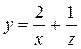 . Произведя замену искомой функции и ее производной на z и
. Произведя замену искомой функции и ее производной на z и 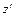 , приведем исходное уравнение Риккати к неоднородному линейному уравнению:
, приведем исходное уравнение Риккати к неоднородному линейному уравнению:
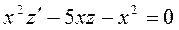 ,
,
или
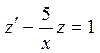 .
.
Интегрируя это уравнение, находим 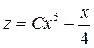 . Следовательно, общее решение исходного уравнения имеет вид:
. Следовательно, общее решение исходного уравнения имеет вид:
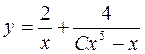 .
.
Частное решение 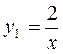 получается из общего при С = ¥.▲
получается из общего при С = ¥.▲
Пример 2.19. Проинтегрировать специальное уравнение Риккати:
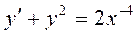 .
.
▲ В этом уравнении т = -4 и условие (2.37) выполнено при k = 1- целом и больше нуля. Следовательно, его можно привести к квадратурам. Произведем замену
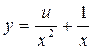 .
.
Тогда получим уравнение
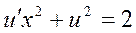 .
.
Разделяя переменные и интегрируя, находим:
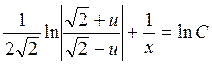 .
.
Возвращаясь к исходным переменным, окончательно будем иметь:
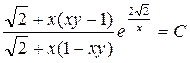 .▲
.▲
Пример 2.20. Найти общее решение уравнения:
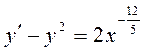 .
.
▲ Это, также как и в предыдущем примере, специальное уравнение Риккати. В этом уравнении т = -12/5 и условие (2.37) выполнено при k = 3. Поэтому в данном случае необходимо провести указанные в А) преобразования трижды. Полагая 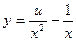 , получаем
, получаем
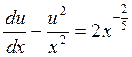 .
.
Произведем замены 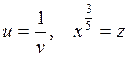 и в результате получим уравнение
и в результате получим уравнение 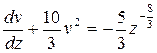 , которое также является специальным уравнением Риккати. Поэтому выполним эти же замены повторно, которые приведут к уравнению
, которое также является специальным уравнением Риккати. Поэтому выполним эти же замены повторно, которые приведут к уравнению 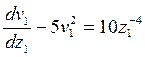 , где
, где 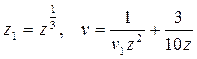 . Применение проведенных преобразований еще раз приводит к уравнению
. Применение проведенных преобразований еще раз приводит к уравнению
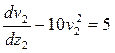 , где
, где 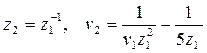
Решая это уравнение, которое уже является уравнением с разделяющимися переменными, найдем:
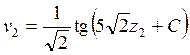 .
.
Возвращаясь к переменным х и у, окончательно получим общее решение исходного уравнения
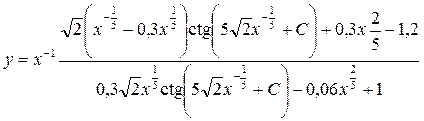 .▲
.▲
Пример 2.21. Кусок рудной массы т падает в рудоспуск под действием силы тяжести, при этом воздух оказывает сопротивление, пропорциональное квадрату скорости падения. Найти закон движения куска.
▲ Пусть s — расстояние, пройденное телом к моменту t. Тогда движение определяется уравнением
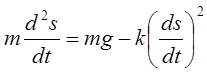
которое может быть представлено в виде
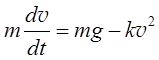 (П.2.21.1)
(П.2.21.1)
где скорость 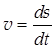 . Дифференциальное уравнение (П.2.21.1) является уравнением Риккати.
. Дифференциальное уравнение (П.2.21.1) является уравнением Риккати.
Разделяя в нем переменные, имеем
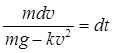
или после сокращения левой части равенства на т
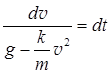
Интегрируя это равенство, получаем
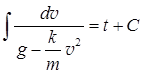 (П.2.21.2)
(П.2.21.2)
Для вычисления интеграла в левой части уравнения (П.2.21.2) применяем метод неопределенных коэффициентов, и тогда
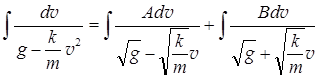 (П.2.21.3)
(П.2.21.3)
Откуда
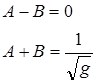
или
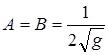
Подставляя найденные значения коэффициентов в интеграл (П.2.21.3), имеем
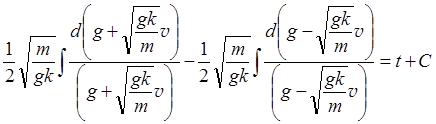
Для краткости обозначим 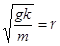 . Тогда после умножения равенства на
. Тогда после умножения равенства на 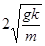 находим
находим
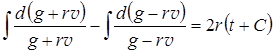
или
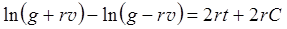
откуда
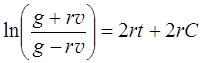 (П.2.21.4)
(П.2.21.4)
Потенцируя уравнение (П.36.4), получаем
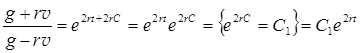
Откуда искомая функция имеет вид
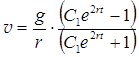
или с учетом того, что 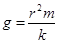 и
и 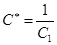 , получим
, получим
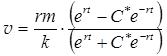 (П.2.21.5)
(П.2.21.5)
Из уравнения (П.2.21.5) очевидно, что при t, стремящемся к бесконечности, скорость v достигает предельного значения
v max= V,
для которого
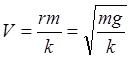
Следовательно, уравнение (П.2.21. 5) записывается в виде
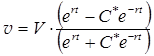 (П.2.21.6)
(П.2.21.6)
Начальное условие: при t = 0 v = v 0.
Пусть ради краткости записи и 0 =v 0 /V. Тогда постоянная интегрирования С* в уравнении (П.2.21.6) принимает значение
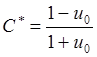
Подставляя это значение в уравнение (П2.21.6), замечаем, что v может быть записана в виде
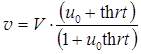
Принимая, что при t = 0 s = 0, можем теперь определить закон движения s:
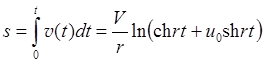
Подставляя 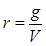 и
и 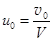 в это равенство, окончательно получаем искомый закон движения
в это равенство, окончательно получаем искомый закон движения
 .▲
.▲
 2014-02-12
2014-02-12 2240
2240
