Задачи для самостоятельной работы

Уравнения с разделенными переменными и приводящиеся к ним

Если в уравнении (1.3) коэффициент M является функцией, зависящей только от x, а коэффициент N является функцией, зависящей только от y, то это уравнение приводится к виду

M(x)dx + N(y)dy = 0, (1.21)

которое называется ОДУ с разделенными переменными. Решение этого уравнения представляется в виде

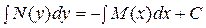. (1.22)

К виду (1.21) можно привести и уравнение (1.3), если каждую из функций M(x,y) и N(x,y) при помощи алгебраических преобразований можно представить в виде произведения двух функций, каждая из которых зависит только от одной переменной:

M(x,y) = f₁(x)·j₂ (y) и N(x,y)= j₁(y)·f₂(x)

Исходя из этого, уравнение (1.3) можно записать в виде

f₁(x)j₂(y)dx + j₁ (y) f₂(x)dy = 0. (1.23)

Полагая, что f₂(x) ¹ 0 и j₂(y) ¹ 0, тогда можно обе части (1.23) умножить на множитель m равный 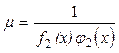. В результате чего уравнение (1.23) примет вид

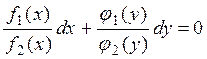. (1.24)

Полученное ОДУ (1.27), также как и уравнение (1.21) будет называться ОДУ с разделенными переменными, а уравнение вида (1.23) будет называться ОДУ с разделяющимися переменными.

Замечание 1. При переходе от уравнения (1.23) к уравнению (1.24) предполагалось, что f₂(x) 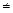0 и j₂(y) 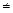0. Однако, для того, чтобы получить полное решение исходного уравнения необходимо также решить и уравнения j₂(y) = 0 и f₂(x) = 0. Решения этих уравнений могут является решениями уравнения (1.23), что проверяется непосредственной подстановкой.

Пример 1.6. Решить ОДУ:

.

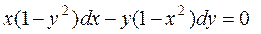▲ При y¹± 1 и x¹± 1 разделяем переменные:

,

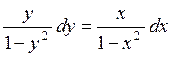интегрируя обе части этого уравнения

,

получаем

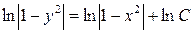, (С ₁>0).

Потенцируя это равенство и, используя свойство модуля, получим

.

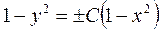Учитывая, что ± С может принимать любые не равные нулю значения, окончательно получаем уравнение семейства интегральных кривых

.

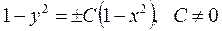При разделении переменных могли быть потеряны решения вида

y =± 1 и х =± 1.

Непосредственной подстановкой убеждаемся, что это частные решения, которые входят в полученную совокупность семейства интегральных кривых как при С = 0, так и при С = ¥, т.к. уравнение 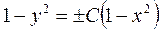можно привести к виду . ▲

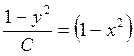Пример 1.7. Найти силу тяги состава с рудой по истечении времени t имеющего начальную скорость v ₀, двигающегося с ускорением прямопропорциональным силе тяги F=b-kv и обратно пропорциональным массе состава с рудой. Если в начальный момент времени при t =0 сила тяги определяется выражением F (t)= F ₀= b-kv ₀.

▲ Скорость движения состава с рудой является функцией времени, т.е. v = v(t), а его ускорение определяется 2-м законом Ньютона

,

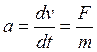где F=b-kv.

Поэтому дифференциальное уравнение исходной задачи будет иметь вид:

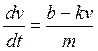. (П7.1)

Разделяя переменные в этом уравнении, получим уравнение с разделенными переменными

,

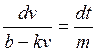Интегрируя которое, найдем общее решение уравнения (П7.1)

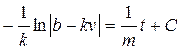или 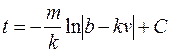(П7.2)

В решении (П7.2) удовлетворим начальному условию – v (0)= v ₀.

.

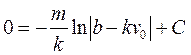
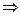
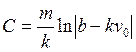Подставив найденное значение постоянной С в общее решение (П7.2), получим решение задачи Коши:

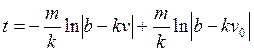
или

.

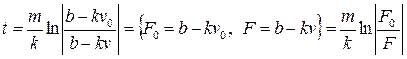Таким образом, искомую силу тяги состава с рудой в любой момент времени, найдем из последнего равенства, избавившись в нем от логарифма

.▲

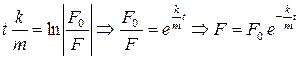Пример 1.8. Трубопровод тепловой магистрали (диаметр 20 см) защищенный изоляцией толщиной 10 см отапливает рабочее помещение при этом температура трубы 160ºС, а внешнего ее покрова 30ºС. Определить распределение температуры внутри изоляции, если коэффициент теплопроводности k = 0,00017, а также количество теплоты, отдаваемой 1 м трубы.

▲ Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то, в соответствии с законом теплопроводности Фурье, количество теплоты, испускаемое в секунду будет равно

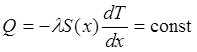(П8.1)

где λ – коэффициент теплопроводности, а площадь сечения тела S(x) определяется по формуле

S(x)=2πxl,

где х – радиус трубопровода, l – длина трубы, следовательно, уравнение (П8.1) можно записать в виде

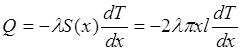
или

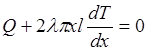(П8.2)

Разделяя переменные в дифференциальном уравнении (П8.2) получим

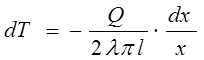(П8.3)

По условию задачи необходимо определить распределение температуры внутри изоляции. Поэтому сначала левую часть уравнения (П8.3) интегрируем в пределах от 160ºС до 30ºС, а правую часть интегрируем в пределах от 10 до 20 см.

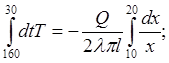
После интегрирования уравнения (П8.3), находим

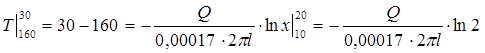(П8.4)

Затем, проинтегрируем левую часть уравнения (П8.3) в пределах от 160ºС до некоторой температуры Т, а правую часть интегрируем в пределах от 10 до х см. После интегрирования уравнения (П8.3), находим

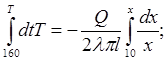
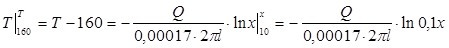(П8.5)

Разделив почленно уравнение (П8.5) на уравнение (П8.4), получим

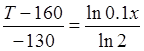
Из этого уравнения следует, что закон распределения температуры внутри изоляции будет иметь вид

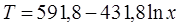
Кроме того, по условию задачи необходимо определить количество теплоты отдаваемой 1 м трубы. Поэтому для того, чтобы выполнить условие задачи необходимо из уравнения (П8.4) при l = 100 см выразить Q и рассчитать его значение

▲

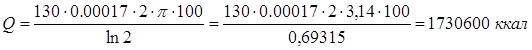Рассмотрим уравнение вида

M(x,y)dx + N(x,y)dy = 0. (1.25)

Если в этом уравнении коэффициенты M(x,y) и N(x,y) являются однородными функциями одного и того же измерения, т.е. выполняются тождества:

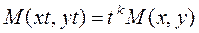и ,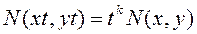

то такое уравнение будет называться однородным и его переменные разделяются посредством подстановки y = zx, где z есть новая неизвестная функция от x. После ее подстановки, а также подстановки значения ее дифференциала: 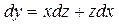, в уравнение (1.25), получим

обозначив 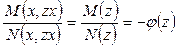, получим уравнение

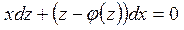, (1.26)

предполагая, что j(z)¹ 0, приходим к уравнению 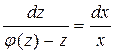, после интегрирования которого, получим общий интеграл уравнения (1.25)

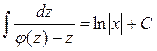или ,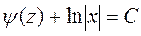

где ,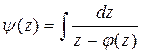

или, возвращаясь к искомой функции у, заменив z на 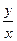, получим общий интеграл уравнения (1.28): .

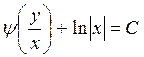В процессе разделения переменных пришлось делить на х и 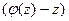, поэтому необходимо рассмотреть еще два уравнения

х =0 и 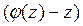=0. (1.27)

Первое уравнение определяет решение уравнения (1.26), которое может оказаться решением уравнения вида

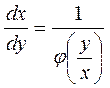
и тогда, решение этого уравнения, должно быть присоединено к решениям уравнения (1.25).

Если второе уравнение из (1.37) имеет действительные решения вида z=α =const, то им соответствуют в силу подстановки y=zx решения однородного уравнения (1.25) вида

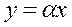(х ¹0)

Эти полупрямые, как и полуоси оси у, о которых шла речь выше, могут оказаться особыми решениями однородного уравнения (1.25).

Пример 1.9. Найти решение уравнения:

.

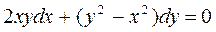▲ Это уравнение является однородным уравнением, т.к. коэффициенты при dx и dy есть однородные функции одного и того же измерения, то есть 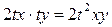и 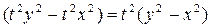. Следовательно, его можно решить, использовав подстановку y=zx. Вычислив dy=xdz+zdx, и подставив в исходное уравнение, получим

.

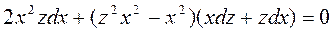Сокращая на x² и собирая члены, содержащие dx и dy, получим

.

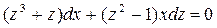Далее разделяя переменные и интегрируя, найдем

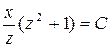
и, возвращаясь к искомой функции у, в конечном итоге получим

.

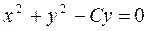Это есть общий интеграл исходного уравнения.

При разделении переменных пришлось сокращать на х ² и делить на (z³+z), поэтому необходимо рассмотреть еще два уравнения, а именно х ² =0 и (z³+z)=0. Первое уравнение дает х = 0, но полуоси у (х = 0 (у ¹0 )) не являются решениями исходного дифференциального уравнения. Из второго уравнения находим z =0 и, подставляя в y=zx, получим

y =0 (x ¹0).

Эти полуоси оси х являются решениями исходного уравнения. Эти решения частные, т.к. во всех точках имеет место единственность решения задачи Коши. ▲

Уравнение вида

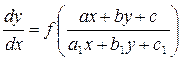, (1.28)

где a,b,c,a₁,b₁,c₁, - постоянные, и для которых выполняется условие

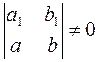, (1.29)

можно привести к однородному уравнению посредством замены переменных

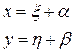, (1.30)

где x и h - новые переменные, а a и b - некоторые постоянные числа, определяемые из системы

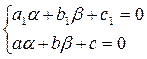. (1.31)

В результате получим уравнение вида

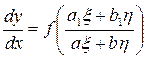. (1.32)

Если же условие (1.29) не выполняется, т.е.

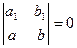, (1.33)

то исходное уравнение (1.28) может быть переписано в виде

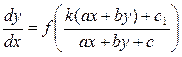, (1.34)

в котором переменные можно разделить с помощью подстановки z=ax+by, где z – новая неизвестная функция от x.

Пример 1.10. Найти решение уравнения

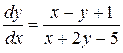. (П1.10.1)

▲ Проверим, выполняется ли условие (1.29)

.

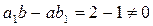Условие выполнено, следовательно, можно записать систему (1.31)

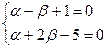, решив которую, можно определить a =1 и b = 2. Таким образом, уравнения (1.30) принимают вид:

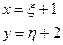. (П1.10.2)

Откуда dx=dx, а dy=dh. Следовательно, внося полученные значения x, y, dx, dy в исходное уравнение получим:

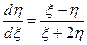или 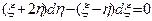. (П1.10.3)

У полученного уравнения (П1.10.3) могут оказаться такие решения, которых нет у исходного уравнения (П1.10.1). Таковыми могут быть лишь те функции, которые обращают в нуль тот множитель, на который мы помножили обе части исходного уравнения.

В данном случае множитель (x+2h) обращается в нуль лишь одной функцией 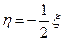, которая не является решением уравнения (П1.10.1).

Уравнение (П1.10.3) есть однородное уравнение, поэтому его можно решать, используя подстановку: h=zx, которая приводит к уравнению

.

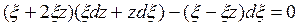В данном уравнении можно разделить переменные. При этом получается уравнение вида:

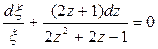, (П1.10.4)

интегрируя которое, получаем

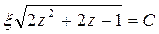. (П1.10.5)

Это есть общий интеграл уравнения (П1.10.4).

Далее подставляем вместо z его выражение 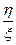, получим общий интеграл уравнения (П1.10.3):

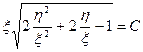или .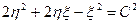

Далее h и x надо заменить согласно равенствам (П1.10.2), после чего общий интеграл исходного уравнения (П10.1) принимает вид:

.▲

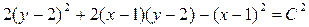Пример 1.11. Решить уравнение

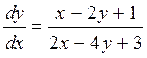. (П1.11.1)

▲ Проверим, выполняется ли условие (1.32)

.

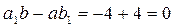Условие (1.29) не выполняется, однако выполнено условие (1.33). Следовательно, исходное уравнение (П1.11.1) можно записать в виде (1.34), а именно

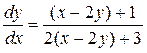. (П1.11.2)

Введем подстановку z=x-2y, откуда вычислим 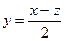и

.

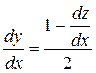Подставляя значения у и 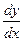в уравнение (П1.11.2), получим:

,

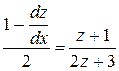и после преобразований будем иметь:

.

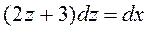Интегрируя это уравнение, получим его общий интеграл: 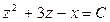, а возвращаясь к исходным переменным, запишем общий интеграл уравнения (П1.11.1):

.▲

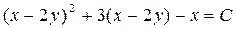Некоторые ОДУ первого порядка можно привести к однородным уравнениям с помощью замены 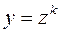, где k –число подлежащее определению. Такие уравнения называются обобщенными однородными уравнениями.

Пример 1.12. Привести уравнение вида 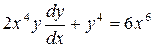к однородному уравнению.

▲ Сделаем замену, 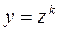после которой исходное уравнение принимает вид:

.

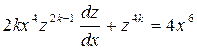Это уравнение будет однородным в случае равенства всех степеней его членов, а именно 4+(2 k -1)=4 k =6. Эти равенства будут выполняться только при k =3/2, поэтому замена 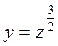приведет исходное уравнение к однородному ОДУ вида:

,

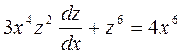которое решается с помощью подстановки z=ux, где u – новая неизвестная функция от х, с учетом того, что 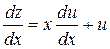будем иметь

,

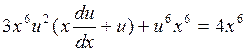или после сокращения на х⁶ получим

.

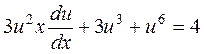Разделив переменные, придем к уравнению 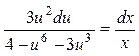, в результате интегрирования которого, получим

.

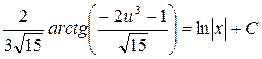Возвращаясь к искомой функции у окончательно запишем общий интеграл исходного уравнения

.▲

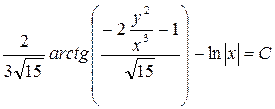Пример 1.13. Найти общий интеграл уравнения:

.

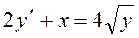▲ Это уравнение не является однородным, но с помощью замены 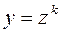мы придем к уравнению вида

.

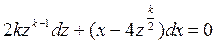Функции 2 kz^{k -1} и (x-4z^k/2) этого уравнения являются однородными и имеют одну и ту же степень при k =2. Следовательно, исходное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки y=x²u(x)

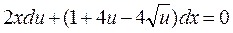, (х³ 0).

Проинтегрировав это уравнение, получим вид общего интеграла 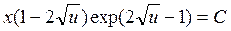или, возвращаясь к искомой функции у, получим общий интеграл исходного уравнения

.▲

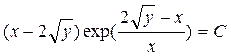Пример. 1.14. Определить уравнение кривой, по которой распола­гается уровень грунтовых вод вблизи скважины, простираю­щейся до непроницаемого слоя (рис.1).

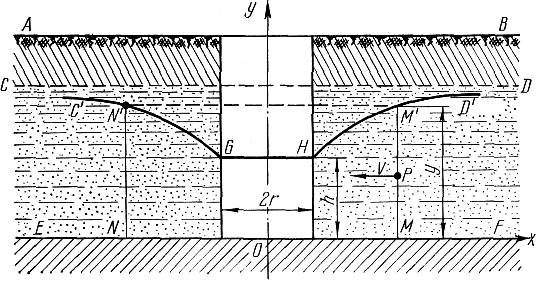
Рис.1.1.

▲ Пусть АВ — поверхность земли; CD — поверх­ность грунтовых вод до устройства колодца; EF — водонепроницае­мый слой, ограничивающий снизу поток грунтовых вод.

Если высота воды в скважине поддерживается откачкой на постоянном уровне GH, то поверхность грунтовых вод вблизи от колодца понижается определенным образом.

Линия поверхности грунтовых вод CD переходит в две искрив­ленные ветки C'G и D'H, которые замыкаются на уровне воды GH. Поверхность уровня грунтовых вод представляет собой поверхность вращения вокруг оси Оу меридиональной линии GC' или HD'.

Кривая HD' определяется на основании эмпирического прави­ла, по которому скорость v течения воды в точке Р пропускающего (дренирующего) грунта пропорциональна наклону кривой в точ­ке М', лежащей на вертикали точки Р.

Обозначая коэффициент пропорциональности через k, получим выражение скорости:

.

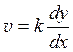
Через боковую поверхность цилиндра 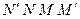радиально внутрь протекает количество воды, определяемое дифференциальным уравнением

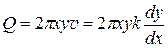, (П1.14.1)

которое для всего цилиндра радиуса х равно расходу воды в скважине.

Разделим переменные в дифференциальном уравнении (П1.14.1):

,

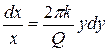Интегрируя, получим

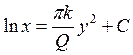(П14.2)

Постоянную интегрирования находим из условия, что кривая поверхности D'H переходит в поверхность скважины GH.

Если диаметр скважины 2 r, а глубина воды в ней h, то при x=r y=h, т.е.

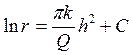
или

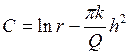(П1.14.3)

Постоянную интегрирования (П1.14.3) вводим в уравнение (П1.14.2) и получаем уравнение искомой кривой

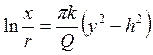
или

. ▲

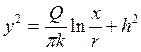Задача 1.15. Резервуар для подготовки суспензии наполнен 75 л смеси воды и трех килограммовсуспезоида. Приток воды составляет 4 л в минуту, а рас­ход смеси из резервуара 2 л в минуту. Концентрация поддерживается равномерной посредством перемешивания (рис.1.2). Найти количе­ство суспензоида, которое будет содержаться в резервуаре через 25 мин.

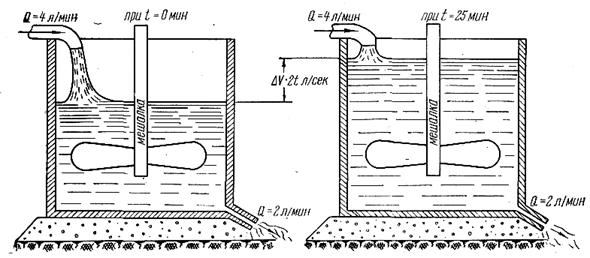
Рис.1.2

▲ Пусть х — количество суспезоида в резервуаре в мо­мент t, кг; t — время, отсчитываемое от начального момента t₀, мин; —dx — количество суспезоида, выходящее из резервуара за время dt (знак минус обусловлен тем, что х — убывающая функция вре­мени), кг.

К моменту t в резервуар поступило 4 t л воды и вышло 2 t л суспензии. Увеличение суспензии составляет 2 t л.

Таким образом, общее количество жидкости достигло 75+2 t л и в ней растворилось х кг суспезоида.

За время dt уходит – dx кг реагента и 2 dt л суспензии.

Считая концентрацию суспензии постоянной, получим количество суспезоида в одном литре 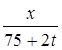кг. Следовательно, за короткий промежуток времени dt количество суспезоида уменьшится на 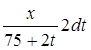кг.

Итак, элементарное уравнение движения жидкости будет иметь вид

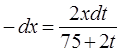
Разделяя переменные в этом уравнении, имеем:

.

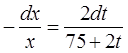Интегрируя это уравнение, с учетом того, что в начальный момент времени t ₀ = 0 в резервуаре было 3 кг суспезоида (х ₀ = 3 кг), а через 25 мин, т.е. в момент времени t ₁= 25 сек, его стало х ₁ = х кг, получим

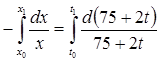
или

.

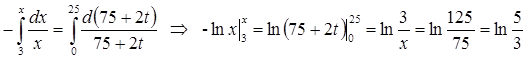Потенцируя полученное выражение, получаем

,

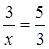или искомое количество суспезоида в резервуаре будет равно

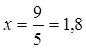кг. ▲

1.1. Найти общий интеграл уравнения:

.

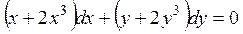1.2. Найти решения уравнения: .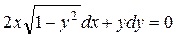

1.3. Проинтегрировать уравнение:.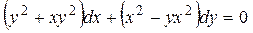

1.4. Проинтегрировать уравнение:.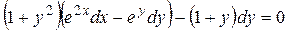

1.5. Решить задачу Коши: .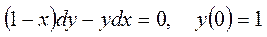

1.6. Найти решение уравнения: 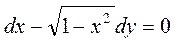и выделить интегральную кривую, проходящую через точку .

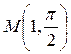1.7. Найти решение уравнения: 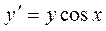, выделить интегральную кривую, проходящую через точку 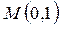, выяснив предварительно вопрос о существовании и единственности этой интегральной кривой.

1.8. Кусок горной массы массой m сбрасывается вниз по рудоспуску. Найти закон изменения скорости падения v этого куска, если на него действует сила тяжести и тормозящая сила сопротивления воздуха, пропорциональная скорости.

Решить уравнения

1.9. .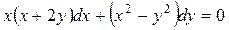

1.10. .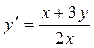

1.11. .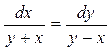

1.12. .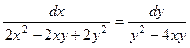

Найти решения вида y = kx.

1.13. 13..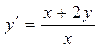

1.14. .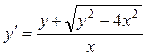

Проинтегрировать уравнения.

1.15. .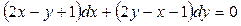

1.16. .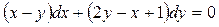

1.17. .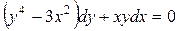

1.18. .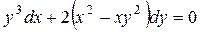

1.19. .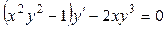

1.20. Найти закон изменения давления куска горной массы на горизонтальную площадь р и стенки транспортной емкости р_S прямоугольной формы с возрастанием глубины h с учетом трения кусков о стенки емкости принимая во внимание, что давление куска на стенки принимается пропорциональным давлению на горизонтальную площадь р_S = kp.

1.21. Подвергая 10 кг соли действию 90 л воды, обнару­жили, что в течение часа растворилась половина этого количества. Считая концентрацию насыщенного раствора соли равной 1/3, най­ти количество растворенной соли в течение часа, если за это время было влито 180 л воды.

1.22. В процессе зарядки коронным разрядом в воздушной или газовой среде происходит процесс ионизации, при котором за 1 сек обра­зуется q положительных и q отрицательных ионов в данном объеме газа. Так как положительные и отрицательные ионы снова соеди­няются между собой, то количество их убывает. Из общего количе­ства п положительных ионов в каждую секунду соединяется часть, пропорциональная квадрату их количества. Коэффициент пропор­циональности k зависит от природы и состояния газа. Найти зави­симость количества ионов п от времени t.

1.23. Для равномерного освещения кусков рудной массы при реализации процесса фотометрической сепарации необходимо определить форму зеркала, чтобы отраженные от него лучи были параллельны оси Ох. Источник света помещен в точке О (рис.1.3).

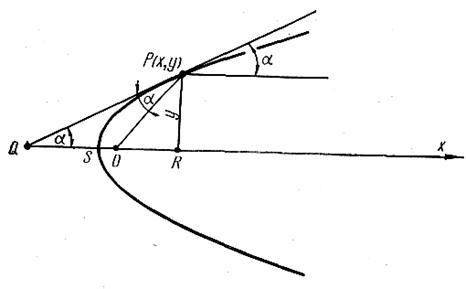
Рис. 1.3