Рассмотрим уравнение
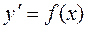 . (1.15)
. (1.15)
Общее решение этого уравнения, если функция f(x) определена и непрерывна в некотором интервале (a,b), может быть представлено в виде
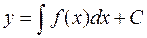 , (1.16)
, (1.16)
и вся область изменения х и у (а< х <b, ½ у ½<+¥) заполнена непересекающимися интегральными кривыми (1.16) уравнения (1.15), причем каждая из них представляет собой график частного решения уравнения (1.15).
Из уравнения (1.16) следует, что все интегральные кривые, входящие в общее решение уравнения (1.15), получаются из какой-либо одной путем ее сдвига вдоль оси О у.
Если поставлена задача Коши, а именно найти решение уравнения (1.15) удовлетворяющее начальным условиям 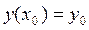 , то такое решение будет иметь вид
, то такое решение будет иметь вид
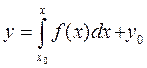 . (1.17)
. (1.17)
Пример 1.4. Найти общее решение уравнения
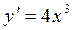 ,
,
и выделить решение, удовлетворяющее начальному условию у = 1 при х = 0.
▲ Очевидно, что правая часть исходного уравнения непрерывна при всех х. Следовательно, общее решение данного уравнения имеет вид
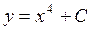 .
.
Это уравнение есть уравнение семейства парабол, которые получаются при сдвиге одной из них параллельно оси О у. Для того, чтобы решить задачу Коши необходимо в полученное решение подставить начальное условие и определить значение произвольной постоянной С: 1=0+ С, откуда С = 1. Следовательно, решение задачи Коши будет иметь вид 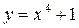 . Таким образом, через точку (0,1) проходит только одна интегральная кривая, определяемая уравнением
. Таким образом, через точку (0,1) проходит только одна интегральная кривая, определяемая уравнением 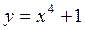 .▲
.▲
Рассмотрим теперь уравнение, не содержащее независимой переменной
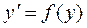 . (1.18)
. (1.18)
Перевернутым для этого уравнения будет уравнение
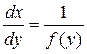 . (1.19)
. (1.19)
Общее решение этого уравнения будет иметь вид
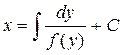 . (1.20)
. (1.20)
Пример 1.5. Найти решение задачи Коши для уравнения
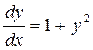 ,
,
удовлетворяющее начальному условию y (0) =0.
▲ Правая часть исходного уравнения непрерывна при всех значениях у и не обращается в нуль, поэтому потери решений быть не может.
Интегрируя исходное уравнение, получим общий интеграл
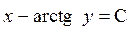 ,
,
а общее решение будет иметь вид
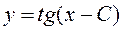
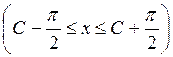 . (П5.1)
. (П5.1)
Следовательно, для того, чтобы определить решение, удовлетворяющее начальному условию у (0)=0, необходимо определить значение произвольной постоянной С. Подставляя в (П5.1) х =0 и у =0 определим, что С =0. Следовательно, решение задачи Коши будет иметь вид:
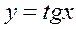
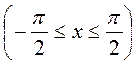 .▲
.▲
 2014-02-12
2014-02-12 435
435








