Принцип сложения

Принципы теории вероятностей.

Напомним, что два события называются несовместными, если они одновременно произойти не могут, то есть, если АВ=Ø и совместными в противном случае. Следующие четыре утверждения и образуют принцип сложения.

Теорема 1. Для любого события 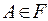имеет место следующее равенство:.

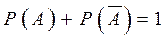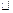. Действительно, так как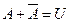, то.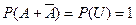

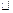
Теорема 2. Если 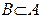, то Р(А-В)=Р(А)–Р(В).

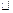Имеем очевидное равенство А=В+(А-В), где В и А-В являются несовместными событиями. Используя аксиому 3 вероятности, имеем Р(А-В)=Р(А)–Р(В).

Теорема 3. (теорема сложения вероятностей). Пусть мы имеем два совместных события А и В. Тогда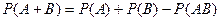

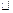Преобразуем их сумму в сумму несовместных событий

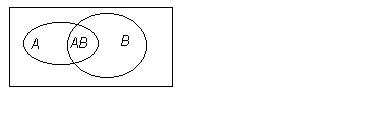
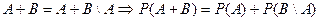
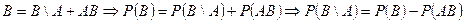
Подставляя второе выражение в первое, получим

.

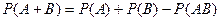Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишень р₁ = 0,7, второго – р₂ = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?

А = А ₁ + А ₂, А попадание в мишень; А₁ – попал первый стрелок; А₂ – попал второй стрелок.

Р(А) =Р(А₁ + А₂)=Р(А₁)+ Р(А₂) –Р(А₁А₂)= Р(А₁)+Р(А₂) – Р(А₁ )Р(А₂)= 0.7+ 0,8 – 0,7· 0,8 = 0,94.

Получим вероятность суммы трех совместных событий.

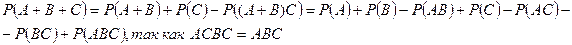
Получена формула

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)

Обобщая полученный результат на сумму n совместных событий, получим формулу

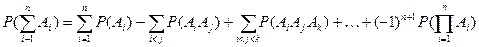
Теорема 4. Для произвольных случайных событий А1, А2, …, Аn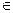F имеет место равенство

.

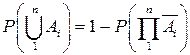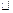. Учитывая, что события 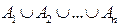и 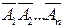являются взаимно противоположными, из теоремы 1 сразу получаем искомое равенство.