Таблица 2
ОКТАНТЫ
Плоскости проекций p1, p2 и p3 являются неограниченными поверхностями и при взаимном пересечении делят пространство на восемь трехгранных углов, или октантов (от лат. octans - восьмая часть).
Нумерация октантов в полупространствах приведена на рис. 12. Знаки координат в каждом из октантов указаны в табл. 2.
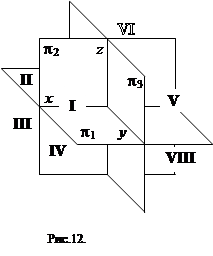 |
| № октанта | x | y | z | Положение в пространстве |
| I | + | + | + | ЛПВ |
| II | + | - | + | ЛЗВ |
| III | + | - | - | ЛЗН |
| IV | + | + | - | ЛПН |
| V | - | + | + | Пр.ПВ |
| VI | - | - | + | Пр.ЗВ |
| VII | - | - | - | Пр.ЗН |
| VIII | - | + | - | Пр.ПН |
Обозначения в таблице: Л – левый октант; Пр. – правый октант; П – передний октант;
З – задний октант; В – верхний октант; Н – нижний октант.
Лекция 2
ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ
 Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и при том только одну.
Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и при том только одну.
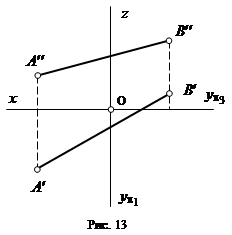
Пусть нам даны на эпюре две точки А и В (рис. 13). Две проекции каждой из этих точек однозначно определяют их положение в пространстве. Если мы соединим одноименные проекции точек, то получим проекции прямой. Точки А и В ограничивают отрезок прямой и определяют положение этой прямой как бесконечной линии.
Таким образом, прямая линия на эпюре может быть задана двумя ее проекциями. По двум проекциям отрезка всегда можно построить его третью проекцию, и притом только одну.
Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям координат. Пример такой прямой изображен на рис. 13.
 2014-02-12
2014-02-12 4788
4788








