Пример 2. Построение третьей проекции точки по двум заданным

1. Даны фронтальная и профильная проекции точки А (рис. 8):

– фронтальная проекция А ¢¢ определяется координатами x_А = | ОА_x |, z_А = | ОА_z |, А ¢¢ = (А_xА ¢¢ ^ x) Ç (А_zА ¢¢ ^ z);

- профильная проекция А ¢¢¢ определяется координатами y_А = | ОА_{y p3}|, z_A = | ОА_z |, А ¢¢¢ = (А_{y p3} А ¢¢¢ ^ y _p3) Ç (А_zА ¢¢¢ ^ z).

2. Из имеющихся проекций проводим линии проекционной связи, перпендикулярные осям проекций и определяем координатные отрезки ОА_x, ОА_y, ОА_z, равные соответствующим координатам точки А:

| ОА_x | = x_А, | ОА_y |= y_А, | ОА_z |= z_{А .}

3. На пересечении линий проекционной связи с осями проекций отмечаем точки А_x, А_yp3, А_z.

4. Строим третью, горизонтальную проекцию точки А – А ¢ (рис. 9). Горизонтальная проекция А ¢ определяется координатами:

x_А = | ОА_x |, y_А = | ОА_{y p1}|, А ¢ = (А_xА ¢ ^ x) Ç (А_{y p1} А ¢ ^ y _p1).

При определении точки А_{у p1}по А_{у p3}перенос осуществляется с оси у _p3на соответствующее по знаку направление оси у _p1.

В зависимости от расположения точки относительно плоскостей проекций различают:

1) точки общего положения, не принадлежащие плоскостям проекций (например, точка А на рис. 6);

2) точки частного положения, лежащие в плоскостях проекций p₁, p₂, p₃, на осях проекций x, y, z или в начале координат.

У точки общего положения все три координаты отличны от нуля.

Если точка лежит в плоскости проекций, то одна из ее координат равна нулю, по оси, перпендикулярной этой плоскости проекций.

Если точка лежит на оси проекций, то две другие ее координаты равны нулю.

Если все три координаты точки равны нулю, то точка лежит в начале координат.

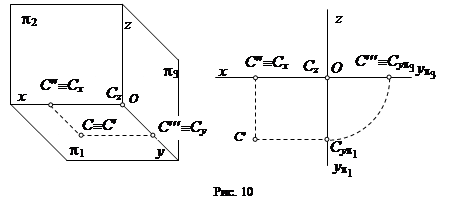
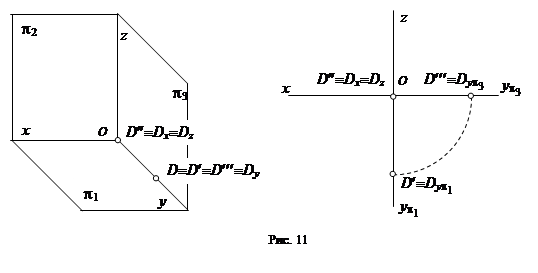
На рис. 10 изображена точка С, принадлежащая горизонтальной плоскости проекций, а на рис. 11 - точка D, лежащая на оси y.