2014-02-12
1000
При выводе этого и предыдущих уравнений используют метод математической физики, который исходит из того, что ограничивается промежуток времени и из всего пространства, выделяется лишь элементарный объём. Это позволяет в пределах элементарного объёма и малого отрезка времени пренебречь изменением некоторых величин и существенно упростить задачу.
Выбранные таким образом элементарные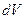 
и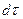 
с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения – величинами ещё достаточно большими, чтобы в их пределах можно было бы игнорировать дискретное строение среды и рассматривать среду как эталонную.
При выводе дифференциального уравнения энергии делают следующие допущения:
- материал однородный и изотропный;
- теплофизические характеристики постоянны;
- внутренние источники тепла распределены по объему равномерно.
В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован таким образом:
|
|
|
Количество тепла, подведенное к элементарному объёму dV за время dt (это dQ*), равно изменению внутренней энергии вещества (dU), содержащегося в данном объёме:
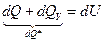, (1.12)
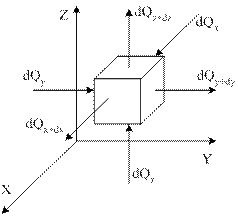| Для нахождения составляющих уравнения (1.12) выделим в теле параллелепипед со сторонами dx, dy, dz. Грани параллелепипеда параллельны соответствующим координатным плоскостям.
Количество теплоты, которое подводится к граням элементарного объёма за время dt в направлении осей Ox, Oy, Оz, обозначим dQx, dQy, dQz,
Общее количество тепла извне: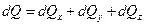
|
Введем понятие потока тепла: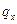 
– количество тепла, проходящего в единицу времени через единицу площади (в данном случае в направлении оси Ox),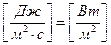 
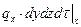– поток, проходящий через сечение x
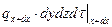– поток, проходящий через сечение x+dx
Разница между количеством теплоты, подведённого к dV за dt и отведённого в направлениях Ox, Oy, Oz может быть выражено:
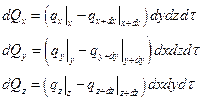(1.13)
Функция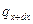 
считается непрерывной в рассматриваемом объёме и может быть разложена в ряд Тейлора:
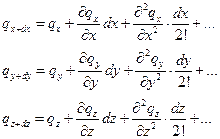(1.14)
Достаточно только два первых члена ряда, подставим (1.14) в (1.13), получим:
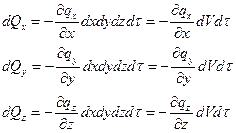
Общее количество теплоты, подведённое к dV за dt:
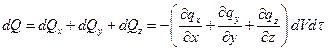
Определим вторую составляющую уравнения (1.12):
Обозначим количество теплоты, выделяемое внутренними источниками в единице объёма среды за единицу времени и называемое мощностью внутренних источников тепла, через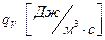 
, тогда:
;
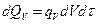Третья составляющая уравнения (1.12) находится для изохорного процесса:
,
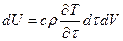где с – теплоемкость*4; r – плотность;
Запишем уравнение (1.12) со всеми изменениями:
или, после сокращения на dVdt
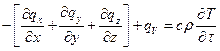(1.13)
Воспользуемся законом Фурье: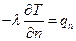 
, подставив его в уравнение (1.13), получим:
|
|
|
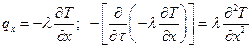
Аналогично подставляем другие члены, в итоге получим:
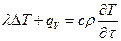– уравнение теплопроводности, где (1.14)
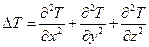
В общем случае теплопереноса (с учётом конвективного и диффузионного механизмов переноса тепла) компоненты теплового потока qx, qy, qz, могут быть представлены:
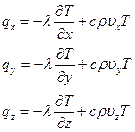(1.15)
Подставив (1.15) в (1.13), получим уравнение энергии:
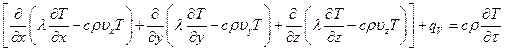
Преобразуем:
Стандартный вид уравнения энергии:
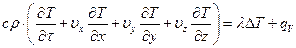(1.16)
В левой части уравнения (1.16) конвективный теплообмен; lDT – молекулярный (диффузионный перенос тепла).
