2014-02-12
889
Получают на основе закона сохранения главного вектора количества движения: изменение главного вектора количества движения (K) во времени в объеме dV равно сумме всех сил, приложенных к этому объему.
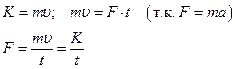
Приравнивая индивидуальную производную по времени от главного вектора количества движения главному вектору внешних массовых и поверхностных сил, получим:
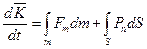
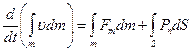
т.к.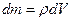 
, а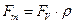 
, то получим:
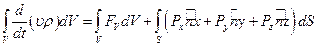
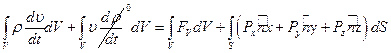(1.6)
В выражении (1.6) будем предполагать, что накопления материала внутри объема не происходит, т.е. r=const, а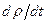 
=0.
Для перехода от поверхностного интеграла к объемному используем теорему Остроградского – Гаусса:
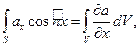
Заменяем последний интеграл в выражении (1.6) и сводим всё под один знак интеграла:
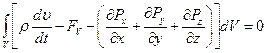
Так как интеграл равен нулю, а dV является малым и виртуальным, то можем приравнять подынтегральной выражение нулю (избавиться от знака интеграла):
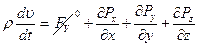
Так как массовые силы в рассматриваемых задачах значительно меньше поверхностных, то ими будем пренебрегать: FV=0:
(1.7)
Спроецируем (1.7) на координатные оси, получим:
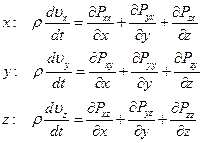
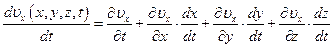
так как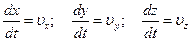 
, то получим:
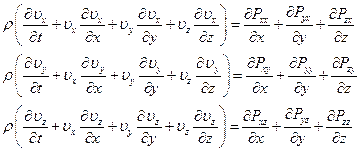(1.8)
Полученные уравнения носят названия – уравнений динамики сплошной среды в напряжениях.
Входящий в уравнение динамики тензор напряжений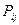 
принято делить на две части и называть полным напряжением.
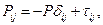*3
где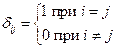 
– символ Кронекера;
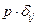– шаровой тензор, отвечающий за изменение объема;
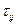– девиатор (девиаторный тензор), отвечает за изменение формы.
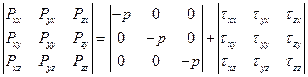(1.9)
С учетом (1.9) правая часть уравнения (1.8) запишется:
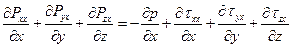
Тогда уравнения движения:
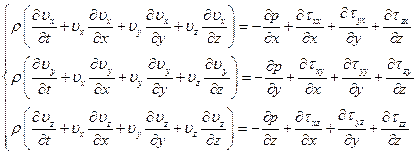(1.10)
Пользуясь численной нумерацией координат, проекций векторов и компонент тензоров, можно представить уравнение (1.10) в компонентной компактной форме:
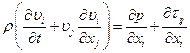(1.11)
Уравнения (1.10) и (1.11) имеют форму второго закона Ньютона. Оно показывает, что скорость изменения количества движения системы равна сумме сил, действующих на неё.
