Метод конечных разностей.
Метод конечных разностей или меток сеток на сегодняшний день является одним из самых распространенных методов приближенного решения краевых задач. Суть метода в следующем:
1. Область непрерывного изменения аргумента заменяется областью дискретного аргумента, выделяются точки, называемые узлами. Наносится сетка.
2. Область непрерывного изменения функции заменяется областью дискретного изменения функции, когда функция определена только в узлах сетки и называется сеточной функцией.
3. Все производные, входящие в определяющие уравнение и краевые условия заменяются (аппроксимируются) алгебраическими соотношениями сеточных функций.
4. Вместо интегрирования дифференциального уравнения записывают разностную схему и решают систему линейных алгебраических уравнений.
При использовании МКР нужно:
1. Выбрать сетку;
2. Выбрать разностную схему;
3. Определить точность аппроксимации;
4. Проанализировать устойчивость и сходимость разностной схемы к точному решению;
5. Провести тестовый расчет.
Свойства разностного решения и, в частности, его близость к точному решению зависит от точного выбора сетки.
Рассмотрим несколько видов сеток.
1. Равномерная сетка
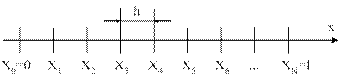 |
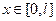 - область изменения аргумента.
- область изменения аргумента.
Разобьем этот отрезок точками 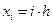 ,
, 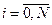 *10 на N равных частей длиной
*10 на N равных частей длиной 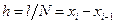 (h – шаг сетки). Таким образом мы задали равномерную сетку в области изменения аргумента. Обозначается:
(h – шаг сетки). Таким образом мы задали равномерную сетку в области изменения аргумента. Обозначается: 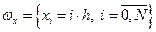
2. Неравномерная сетка получается в том случае, когда 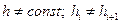 ,
,
пример: 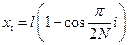
3. Сетка на плоскости.
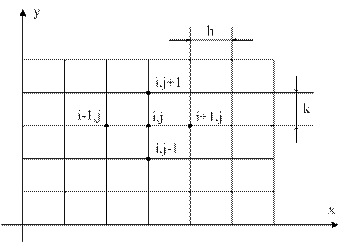 | Если шаги сетки по каждому из переменных (x, y) одинаковы, то сетка называется равномерной. Если же хотя бы по одной переменной шаг непостоянен, то сетка – неравномерная. Введение сетки: 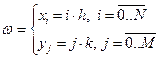 |
Метод конечных разностей сводится к замене производных, входящих в уравнения и краевые условия, разностными отношениями.
Классическое определение производной функции одной переменной записывается в виде:
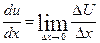
Разложим функцию U в ряд Тейлора в окрестностях точки x0
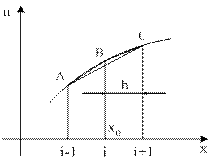 | 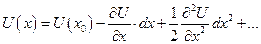 Положим, что Положим, что 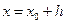 , получим: , получим: 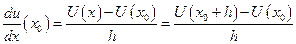 *11 Это равенство называется правой разностью. *11 Это равенство называется правой разностью. |
Другая форма записи правой разности:
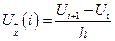
Если 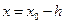 , то получим левую разность:
, то получим левую разность:
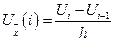
Существует также третья форма записи разностного отношения, называемая центральной разностью:
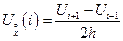
Если задана функция u(x), то графически интерпретация производных трёх типов содержат:
AB – левая разность;
CB – правая разность;
АС – центральная разность.
Узлы, которые задействованы в аппроксимации производной, называются шаблонами аппроксимации.
Получим разностное соотношение для второй производной: 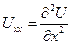
Сначала представим Uxx через Ux, используя правую разность:
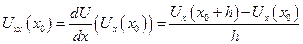 (5.1)
(5.1)
Далее производные 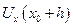 и
и 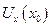 рассмотрим через левую разность для того, чтобы конечный результат не был смещен вправо, т.е. чтобы не было погрешности.
рассмотрим через левую разность для того, чтобы конечный результат не был смещен вправо, т.е. чтобы не было погрешности.
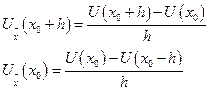 (5.2)
(5.2)
Подставив (5.2) в (5.1), получим:
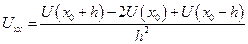
С использованием сетки вторая производная имеет вид:
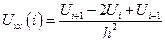
 2014-02-12
2014-02-12 6623
6623
