Пример № 5.1

Имеем уравнение теплопроводности стационарное и одномерное. Численное решение этого уравнения с помощью метода конечных разностей:

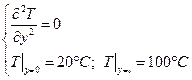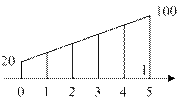Сетка: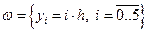

Система уравнений после подстановки:

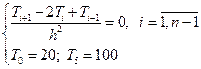или то же самое: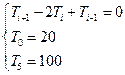

Запишем уравнения для каждого узла:

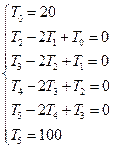
В этой системе уравнений 4 уравнения, 4 неизвестных, т.е. она решаемая.

Матрица коэффициентов (трехдиагональная матрица):

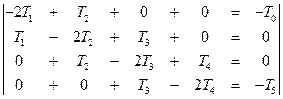
Если бы разбили на 100 элементов, получили бы 98 уравнений.

Такая матрица называется разреженной. Существуют специальные методы для решения систем линейных алгебраических уравнений с разреженными матрицами. Из прямых методов решения наиболее используемый – метод прогонки. Из итерационных – метод Гаусса-Зейделя.

Прямой метод – получение треугольной матрицы.

Метод Гаусса-Зейделя:

Пусть имеется 2 уравнения:

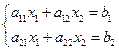
Выделяем диагональные члены:

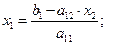(5.3)

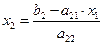(5.4)

Подставляются любые значения:

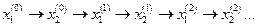
Т.е. берем любое число, подставляем в (5.3) вместо x₂, находим 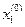. Этот 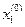подставляем в уравнение (5.4) и находим 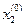, дальше 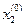подставляем в (5.3) и находим …

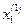Это продолжается до тех пор, пока погрешность будет меньше заданной величины:

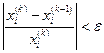
Итерационный метод сходится, если диагональные коэффициенты матрицы больше чем соседние, например:

Система 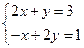решается, а система с переставленными строками – нет:

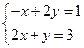
Нестационарные задачи теплопроводности.

В зависимости от того, как выбраны разностные соотношения для производных по времени и координатам получают разностные схемы, которые подразделяют на:

- явные разностные схемы

- неявные разностные схемы

Преимуществом явных является простота выражения неизвестных, которые определяются явно, т.е. сразу из уравнения. Недостатком явных разностных схем является условная её устойчивость, т.е. не для любого соотношения шагов по времени и координатам решение может быть получено. Для каждой конкретной задачи определяется свое соотношение шагов.

В неявных разностных схемах неизвестные определяются путем решения систем линейных алгебраических уравнений на каждом временном слое, т.е. отсутствует простота определения неизвестных, в отличие от явных схем, и это является недостатком. Достоинством же является безусловная устойчивость, т.е. нет ограничений по выбору шагов по времени и координатам.