Из определения следует, что

Задача 2.

Задача 1.

Распределение случайной величины X заданно рядом распределения. Найти неизвестное p₃, построить функцию распределения (записать в аналитическом и графическом виде).

X	–1
P	0,3	0,2	?	0,1

Решение. Все возможные значения случайной величины X образуют полную группу событий, следовательно, сумма их вероятности равна единице. Отсюда p₃ = 1 – (0,3 + 0,2 + 0,1) = 0,4.

Тогда ряд распределения будет иметь вид

X	¾1
P	0,3	0,2	0,4	0,1

Найдем теперь функцию распределения. Согласно определению F(x) = P(X < x). В нашей задаче случайная величина может принять 4 значения, поэтому решение разобьется на 5 случаев:

а) x ≤ –1, тогда F(x) = P (X < –1) = 0,так как X не имеет значений, меньших –1;

б) –1 < x ≤0, тогда F(x) = P (X < 0) = P (X = –1) = 0,3;

в) 0 < x ≤ 2, тогда F(x) = P (X < 2) = P (X = –1)+ P (X =0) = 0,3 + 0,2 = 0,5;

г) 2 < x ≤ 3, тогда F(x) = P (X < 3) = P (X = –1)+ P (X = 2)+ P (X = 2) = 0,3 + 0,2 + 0,4 = 0,9

д) x > 3, тогда F(x) = P (X = –1) + P (X = 2) + P (X = 2) + P (X = 3) = 0,3 + 0,2 + 0,4 + 0,1 = 1.

Запишем функцию в аналитическом виде:

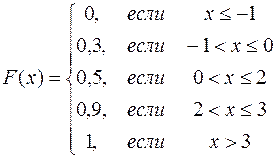
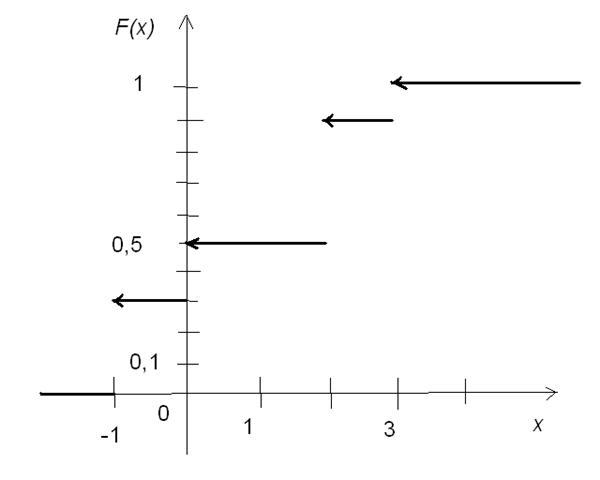
В графическом виде функция распределения выглядит следующим образом:

Вероятность брака некоторой детали равна 1/4. Для проверки случайным образом выбрали три детали. Построить ряд распределения и функцию распределения числа годных деталей среди выбранных. Функцию распределения записать в аналитическом и графическом виде.

Решение. Обозначим X – количество бракованных деталей. Случайная величина X может принять значения 0, 1, 2, 3. Далее нужно найти вероятности каждого значения. Используем формулу Бернулли (n = 3, так как выбрали три детали; m принимает значения 0, 1,2, 3, соответственно; вероятность того, что деталь бракованная равна 1/4; вероятность того, что деталь годная равна 1 – 1/4 = 3/4).

Получаем, P₁=C₃ × (3/4) × (1/4)³ = 0,0156; P₂ = С₃¹ × (3/4)¹ × (1/4)² = 0,1406; P₃ = C₃² × (3/4)² × (1/4)¹ = 0,4219; P₄ = С₃³ × (3/4)³ × (1/4)° = 0,4219.

Ряд распределения имеет вид

X
P	0,0156	0,1406	0,4219	0,4219

Найдем функцию распределения и запишем ее сразу в аналитическом виде.

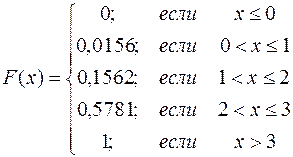
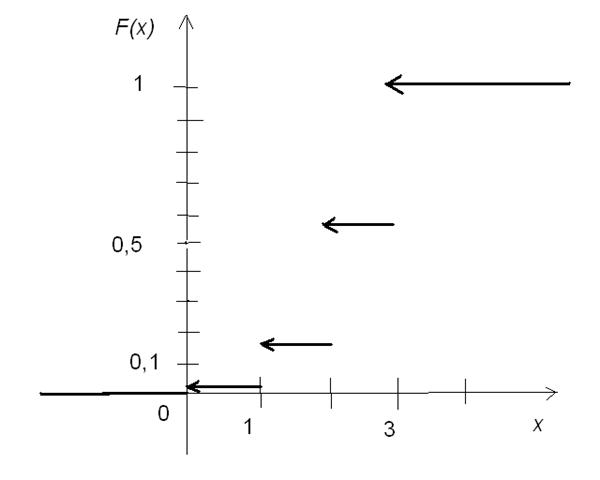
В графическом виде:

§ 2 Числовые характеристики дискретной случайной величины

Закон распределения полностью описывает случайную величину с вероятностной точки зрения. Но при решении ряда задач нет необходимости знать все вероятностные характеристики, достаточно лишь некоторых количественных показателей, которые в сжатой форме давали бы достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины.

Математическим ожиданием М(Х) дискретной случайной величины Х называется число, равное сумме произведений всех возможных значений случайной величины на вероятность этих значений:

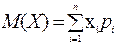
Математическое ожидание характеризует положение случайной величины на числовой оси, определяя собой некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.

Свойства математического ожидания.

1. Математическое ожидание суммы двух случайных величин равно сумме из математических ожиданий, т.е. M(X+Y)= M(X) + M(Y).

2. Математическое ожидание константы равно константе, т.е. M(С) = С.

3. Постоянный множитель случайной величины можно выносить за знак математического ожидания, т.е. M(СX) = СM(X).

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее среднего значения, т.е. D(X) = M(X – M(X))².

Для дискретной случайной величины справедлива формула

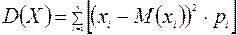
Недостатком дисперсии является то, что она имеет размерность квадрата. Чтобы избавиться от этого, вводят понятие среднеквадратичного отклонения.

Среднеквадратичным отклонением s(Х) случайной величины Х называется арифметический корень из ее дисперсии, т.е.

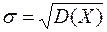
C помощью этих двух величин можно судить о рассеивании значений случайной величины вокруг ее математического ожидания.

Свойства дисперсии.

1. Для любой случайной величины Х дисперсия является неотрицательной величиной.

2. Дисперсия постоянной величины равна нулю, т.е. D(С) = 0.

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания, т.е. D(X) = M(X²) – (M(X))².

4. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат, т.е. D(СX) = С²D(X).

Задача.

Из ящика, содержащего 2 белых и 3 красных шара, вынимают 2 шара. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение числа вынутых белых шаров.

Решение. Пусть Х – количество вынутых белых шаров. Х может принимать значения 0, 1, 2. Найдем соответствующие вероятности, воспользовавшись формулой Бернулли (n = 2, так как достают 2 шара; m меняет свои значения от 0 до 2; вероятность достать белый шар p = 2/5; q = 1 – p = 3/5).

P₁ = C₂⁰(2/5)⁰(3/5)² = 0,36

P₂ = C₂¹(2/5)¹(3/5)¹ = 0,48

P₃ = C₂²(2/5)²(3/5)⁰ = 0,16

Проверка: P₁ + P₂ + P₃ = 0,36 + 0,48 + 0,16 = 1.

Получили следующий ряд распределения:

X
P	0,36	0,48	0,16

Теперь по формуле найдем математическое ожидание

M(X) = 0×0,36+1×0,48+2×0,16=0,8.

Находим дисперсию по формуле

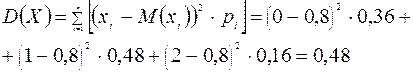
Можно найти дисперсию другим способом, воспользовавшись формулой из свойства 3: D(X) = M(X²) – (M(X))².

M(X²) = 0²×0,36 + 1²×0,48 + 2²×0,16 = 1,12.

D(X) = 1,12 – 0,82 = 0,48.

Теперь можем найти среднеквадратичное отклонение

.

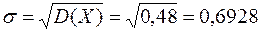Ответ: M(X) = 0,8; D(X) = 0,48; s(X) = 0,69.

§ 3. Непрерывные случайные величины

Непрерывной называется случайная величина, возможные значения которой непрерывно заполняют некоторый заданный промежуток и у которой ее функция распределения представляет собой функцию, непрерывную во всех точках данного промежутка.

Как видно из определения, непрерывная случайная величина принимает значения из некоторого интервала, таких значений бесконечно много и их нельзя пересчитать. Непрерывные случайные величины получаются, например, когда имеют дело с результатами наблюдений.

При рассмотрении этих величин возникает так называемый парадокс непрерывности. Он состоит в том, что при очень большом числе опытов случайная величина будет принимать какое-либо конкретное значение очень редко, так что относительная частота этого события будет приближаться к нулю. Таким образом, вероятность каждого отдельно взятого значения случайной величины будет равна нулю. В связи с этим случайная величина не может быть охарактеризована вероятностями своих значений.

В связи с этим для характеристики случайной величины вводится новая функция, которая называется плотностью вероятности или плотностью распределения случайной величины X.

Пусть Х — непрерывная случайная величина, имеющая дифференцируемую функцию распределения F(х) на всей числовой оси. Функцией плотности вероятности для Х в точке х называется функция f(x), определяемая равенством

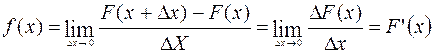
Свойства плотности вероятности.

1. Для любого х плотность вероятности f(х) неотрицательна.

2. Вероятность попадания случайной величины Х в интервал 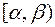равна

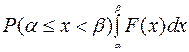
3. Если F(x) и f(x) соответственно функции распределения и плотности вероятности, то

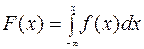
4. Если f(x) – плотность вероятности, то

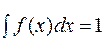
Рассмотрим самое простое непрерывное распределение.

Случайная величина Х называется равномерно распределенной на отрезке [a, b], если плотность распределения вероятности этой величины постоянна на отрезке [a, b] и равна нулю вне этого отрезка.

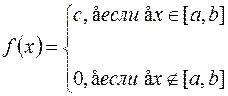
Используя свойство 4, найдем константу с.

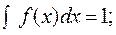
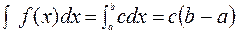
Получаем, что с(b – a) = 1, отсюда с = 1/(b – a).

Следовательно,

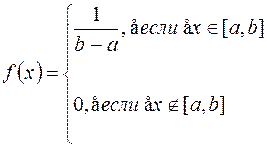
Функция распределения будет иметь вид (по свойству 3):

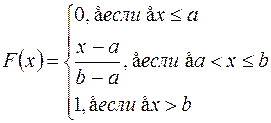
Вероятность попадания случайной величины Х в интервал [ c, d ], принадлежащий [ a, b ] находится по формуле (использовали свойство 2):

P (c < x < d) = (d – a)/(b – a).

Математическое ожидание и дисперсия соответственно равны

M(Х) = (b + a)/2; D(Х) = (b – a)²/12.