2014-02-12
2883
Задача 3.
Задача 2.
Задача 1.
Задача 3.
Задача 2.
Задача 1.
Задача 4.
Задача 3.
Задача 2.
Задача 1.
Стрелок делает выстрел по мишени. В 24 случаях из 100 он попадает в область 1, в 17 случаях — в область 2. Какова вероятность того, что стрелок попадет в одну из областей?
Решение. Пусть событие А — стрелок попал в первую область, В — попал во вторую область. Тогда искомое событие состоит из суммы А и В. События несовместны, так как стрелок не может попасть сразу в обе области при одном выстреле. Используем теорему суммы для несовместных событий. Р(А+В) = Р(А) + Р(В) = 24/100 + 17/100 = 0,41.
Ответ: искомая вероятность равна 0,41.
Два стрелка делают по одному выстрелу по одной мишени. Какова вероятность поражения мишени, если первый стрелок попадает в половине случаев, а второй — в трети.
Решение. Обозначим А — попал первый, В — попал второй. Тогда искомое событие представляет собой сумму А и В. Из условия задачи видно, что А и В совместны, так как оба стрелка могут попасть в цель. Используем формулу суммы совместных событий Р(А+В) = Р(А) + Р(В) — Р(АВ).
|
|
|
По условию Р(А) = 1/2, Р(В) = 1/3.
События независимы, так как попадание одного не зависит от попадания другого, следовательно, Р(АВ) = Р(А)Р(В) = 1/2 × 1/3 = 1/6.
Получаем, что Р(А+В) = 1/2 + 1/3 — 1/6 = 2/3.
Ответ: искомая вероятность равна 2/3.
Какова вероятность того, что при бросании монеты 4 раза всегда будет выпадать «орел»?
Решение. Обозначим событие А1— выпадение орла при первом бросании, А2— при втором, А3— при третьем, А4— при четвертом. Искомое событие состоит из появления всех событий, т.е. является их произведением. События А1, А2, А3, А4независимы, так как выпадение «орла» в первом случае не изменит вероятности выпадения «орла» во всех остальных и т.д. Поэтому используем формулу вероятности произведения независимых событий.
Р(А1А2А3А4) =Р(А1)Р(А2)Р(А3)Р(А4)=1/2 × 1/2 × 1/2 × 1/2 = 1/16.
Ответ: искомая вероятность равна 1/16.
Из колоды карт (52 шт.) поочередно достают 3 карты. Какова вероятность того, что это будут тройка, семерка, туз?
Решение. Пусть А1— первый раз достали тройку; А2— второй раз достали семерку; А3— третий раз достали туз. Искомое событие состоит из появления всех событий, т.е. является их произведением. А1,А2, А3зависимы, так как когда мы достанем одну карту, количество карт в колоде уменьшится и вероятность второго события изменится, аналогично для третьего события. Следовательно, необходимо применить Теорему 7.
Получим, что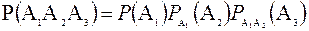 
Найдем нужные нам условные вероятности по классическому определению.
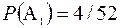(n = 52, так как в колоде 52 карты; m = 4, так как в колоде четыре тройки);
|
|
|
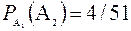(n = 51, так как одну карту уже достали);
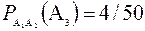(n = 50, так как уже достали две карты).
Отсюда получаем, что P(А1А2А3) = 4/52 × 4/51 × 4/50 = 0,0005.
Ответ: вероятность достать из колоды карт тройку, семерку, туз равна 0,0005.
§ 4. Формулы полной вероятности и Байеса
ТЕОРЕМА 1. Вероятность Р(А) появления события А, которое может произойти совместно только с одним из событий В1, В2,…, Вn, образующих полную группу событий, находится по формуле
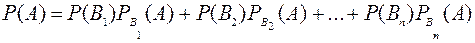
Эта формула называется формулой полной вероятности.
События В1, В2,…, Вn, образующие полную группу, называются гипотезами.
ТЕОРЕМА 2. Если до опыта вероятности гипотез были Р(В1), Р(В2),…, Р(Вn), а в результате опыта появилось событие А, то условные вероятности гипотез вычисляются по формуле
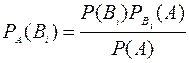
где Р(А) – полная вероятность события А.
Эта формула носит название формулы Байеса. Формула Байеса дает возможность «пересмотреть» вероятности гипотез с учетом наблюдаемого результата опыта.
На сборочный конвейер поступают детали с трех станков. Первый дает 50% деталей, второй – 30%, третий – остальные. Если в сборку попадет деталь первого станка, то вероятность получения годного узла равна 0,98; для второго и третьего станков эти вероятности соответственно равны 0,95 и 0,8. найти вероятность того, что произвольно выбранный узел окажется бракованным.
Решение. Обозначим А – узел бракованный. Качество узла зависит от того, с какого станка поступила деталь, т.е. гипотезы состоят в следующем: В1 – деталь с первого станка; В2 – деталь со второго станка; В3 – деталь с третьего станка.
Необходимо использовать формулу полной вероятности. Найдем соответствующие вероятности.
Р(В1) = 0,5 (так как первый станок дает 50% изделий);
Р(В2) = 0,3 (так как второй станок дает 30% изделий);
Р(В3) = 0,2 (так как третий станок дает 100%-50%-30% = 20% изделий);
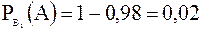(так как нам дана вероятность получения годного узла, а мы ищем вероятность противоположного события – получение бракованного узла);
;
.
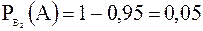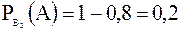Теперь подставляем полученные значения в формулу полной вероятности.
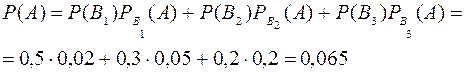
Ответ: вероятность того, что узел окажется бракованным, равна 0,065.
В условиях задачи 1 найти вероятность того, что бракованная деталь оказалась изготовлена на втором станке.
Решение. Нам необходимо перечислить вероятность гипотезы В2, при условии, что узел оказался бракованным. Следовательно, нужно использовать формулу Байеса для В2.
.
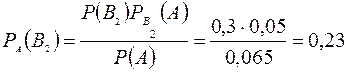Ответ: вероятность того, что деталь сделана на втором станке, равна 0,23.
Имеется 3 ящика с шарами. В первом находится 8 белых и 4 черных шара, во втором – 4 белых и 6 черных, в третьем – 10 белых и 5 черных. Наугад достают один шар из любого ящика. Какова вероятность того, что он окажется черным?
Решение. Обозначим А – вынули черный шар. Гипотезами, т.е. событиями совместно с одним из которых может появиться событие А, являются В1 – шар из первого ящика, В2 – шар из второго ящика, В3 – шар из третьего ящика.
Найдем соответствующие вероятности.
Р(В1) = Р(В2) = Р(В3) = 1/3 (так как В1, В2, В3 равновозможные в условиях данной задачи и образуют полную группу).
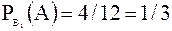(использовали формулу классического определения);
;
.
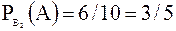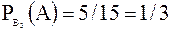Подставляем полученные значения в формулу полной вероятности
P(A) = 1/3×1/3 + 1/3 × 3/5 + 1/3 × 1/3 = 19/45.
Ответ: искомая вероятность равна 19/45.
§ 5. Схема испытаний Бернулли
Пусть в результате некоторого опыта может появиться определенное событие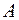 
с вероятностью 
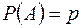. Этот опыт повторяется в одинаковых условиях 
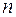раз (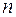– фиксированное число). Вероятность наступления события 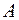в каждом из этих испытаний одна и та же и исход любого испытания не зависит от результатов других опытов. Такую последовательность независимых испытаний с двумя исходами (появление 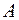, не появление 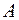) называют схемой Бернулли.
Пример.
Монету бросают n раз, событие 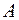– выпадение «орла», 
.
|
|
|
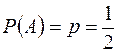Всякий исход такой последовательности независимых испытаний есть чередование 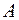и 
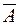в произвольном порядке и в произвольном наборе. Вероятность события 
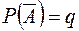определяется по формуле 
.
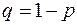Пусть нас интересует вероятность того, что в серии из 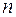опытов событие 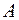появится ровно 
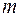раз. На этот вопрос отвечает
ТЕОРЕМА. Если производится последовательность 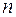независимых испытаний, в каждом из которых с вероятностью 
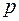наступает событие 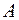, то вероятность 
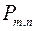того, что в этих 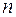испытаниях событие 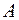произойдет 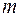раз, определяется по формуле
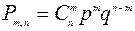, где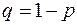
Эта формула называется формулой Бернулли.
Следствие. Сумма вероятностей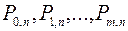 
равна единице, т.е.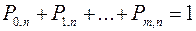 
Это следствие часто используется для проверки сделанных вычислений.
В задачах, связанных со схемой Бернулли, часто возникает необходимость найти наиболее вероятное количество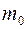 
наступлений события . Его определяют из двойного неравенства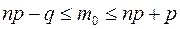 
.
Вероятность выхода за допустимые границы при обработке детали равна 0,07. Какова вероятность того, что из пяти наугад отобранных деталей у двух размеры не соответствуют заданному диапазону?
Решение. Пусть 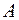– размеры не соответствуют заданному диапазону. По условию 
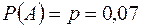. Тогда 
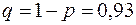. Количество опытов 
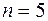так как выбрали пять деталей; 
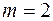. Используя формулу Бернулли, получим искомую вероятность
.
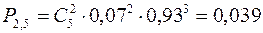Ответ: искомая вероятность равна 0,039.
В условиях задачи 1 найти вероятность того, что у двух деталей размеры соответствуют заданному диапазону.
Решение. Пусть 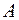– размеры соответствуют диапазону. Тогда получаем, что по условию нам дана вероятность противоположного события, т.е. 
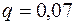. Отсюда 
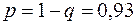. Величины 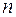и 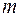остались без изменений. Подставляем все в формулу Бернулли
.
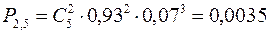Ответ: искомая вероятность равна 0,0035.
Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?
Решение. Пусть 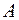– день дождливый. Количество опытов 
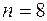, так как рассматривается 8 дней; 
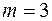. Найдем вероятность того, что произвольный день дождливый, т.е. 
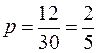(использовали формулу классической вероятности). Тогда 
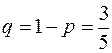. Применяем формулу Бернулли
|
|
|
.
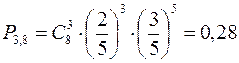Ответ: искомая вероятность равна 0,28.
Задача 4.
Вероятность того, что на предприятии расход электроэнергии превысит суточную норму равна 0,2. Какова вероятность того, что в течении не менее 5 дней из 7 перерасхода не будет?
Решение. Обозначим 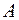– перерасхода нет в какой-либо день, 
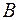– нет перерасхода не менее 5 дней из 7. Тогда 
; 
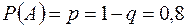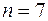. Далее решение придется разбить на три случая:
a) перерасхода нет 5 дней, т.е.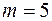 
;
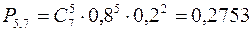b) перерасхода нет 6 дней, т.е.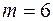 
;
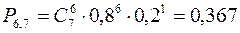c) перерасхода нет 7 дней, т.е.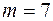 
.
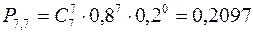Искомая вероятность представляет собой сумму вероятностей в рассмотренных случаях, следовательно,
.
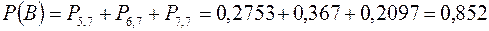Ответ: искомая вероятность равна 0,852.
Задача 5.
Всхожесть семян данного растения равна 0,8. Найти наиболее вероятное число проросших семян из 5 посеянных.
Решение. Обозначим 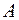¾ семя взошло, 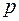¾ вероятность 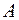. Согласно условию 
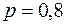, количество испытаний 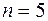. Тогда 
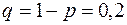. Воспользуемся неравенством для наивероятнейшего количества появления события : 
, 
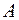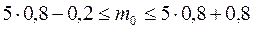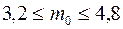. Единственное натуральное число, удовлетворяющее этому неравенству, равно 4, следовательно, 
.
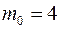Ответ. Наиболее вероятное количество проросших семян из посаженных равно 4.
Формула Пуассона
Если в схеме Бернулли количество испытаний 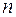велико, вероятность 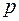события 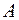в одном испытании мала, а произведение 
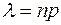не превосходит 20, то вероятность того, что событие появится ровно в 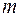испытаниях, определяется по приближенной формуле Пуассона: 
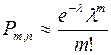. Для использования формулы Пуассона обычно достаточно выполнения условий 
, 
.
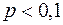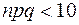Значения распределения Пуассона имеются в специальных таблицах.
Задача 6.
В ходе проверки аудитор случайным образом отбирает 10 счетов. Найти вероятность того, что он обнаружит один счет с ошибкой, если в среднем 3% счетов содержат ошибки.
Решение. В нашем случае количество испытаний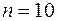 
, вероятность ошибки в одном испытании 
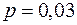. Тогда 
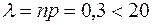и можно применить формулу Пуассона: 
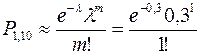. Вычислять это выражение нет необходимости, достаточно воспользоваться специальными таблицами.
Ответ. Вероятность обнаружить один счет с ошибкой равна 0,2223 или 22%.
Локальная формула Муавра-Лапласа
Если в схеме Бернулли число испытаний 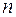велико, а вероятност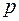и и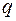 
не очень близки к нулю (обычно достаточно условий 
, 
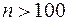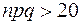), то вероятность наступления события 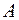ровно 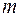раз можно найти по локальной формуле Муавра-Лапласа: 
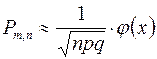, где 
, 
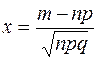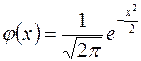¾ функция Гаусса, значения которой имеются в специальных таблицах. Следует заметить, что функция Гаусса четна, то есть 
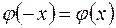, поэтому в таблице приводятся данные только для положительных значений аргумента.
Задача 7.
Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 180 грибов белых будет 40?
Решение. В нашем случае количество испытаний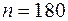 
, 
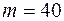, вероятность 
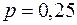. Проверяем условие применимости локальной формулы Муавра-Лапласа: 
, 
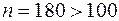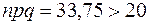. Формулу можно применить.
Найдем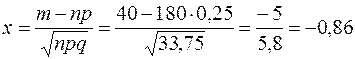 
. Для вычисления 
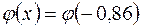воспользуемся таблицей, получаем 
.
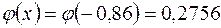Тогда искомая вероятность равна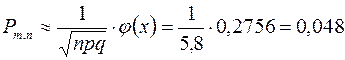 
Ответ. Вероятность собрать ровно 40 грибов из 180 примерно равна 5%.
Интегральная формула Муавра-Лапласа
В условиях локальной формулы Муавра-Лапласа вероятность того, что число 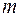наступления события 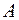находится в заданном промежутке 
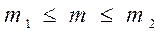вычисляется по формуле: 
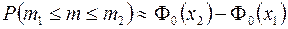, где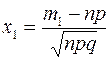 
, 
, 
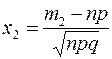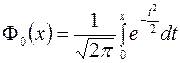¾ функция Лапласа, значения которой имеются в специальных таблицах. Следует заметить, что функция Лапласа нечетна, то есть 
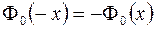, поэтому в таблице приводятся данные только для положительных значений аргумента.
Задача 8.
В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью 0,25. Какова вероятность того, что количество спелых арбузов будет находится в пределах от 564 до 600.
Решение. В нашем случае количество испытаний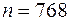 
, 
, 
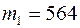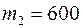, вероятность 
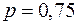. Проверяем условие применимости формулы Муавра-Лапласа: 
, 
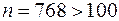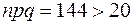. Формулу можно применить.
Найдем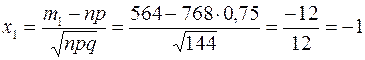 
, 
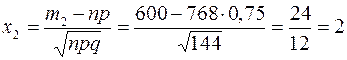. Для вычисления значений функции Лапласа воспользуемся таблицей, получаем 
, 
.
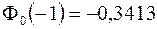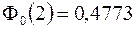Тогда искомая вероятность равна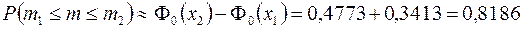 
Ответ. Искомая вероятность примерно равна 82%.
С помощью интегральной формулы Муавра-Лапласа можно получить формулу вероятности отклонений относительной частоты от постоянной вероятности в 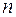независимых испытаниях не более чем на число 
: 
.
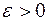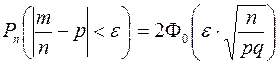Задача 9.
Сколько раз надо подбросить монету, чтобы с вероятностью 90% относительная частота появления герба отличалась от его классической вероятности не более чем на 1%?
Решение. Воспользуемся формулой 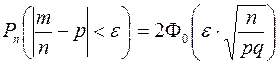, где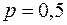 
¾ классическая вероятность выпадения герба, 
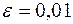¾ заданная степень погрешности.
Получаем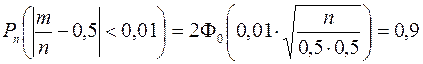 
, откуда 
, 
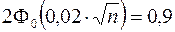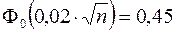. Далее. воспользовавшись таблицей функции Лапласа, получаем 
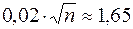, следовательно, 
.
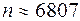Ответ. Монету нужно подбросить примерно 6807 раз.
РАЗДЕЛ II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 1. Дискретные случайные величины
Стремление использовать числа при анализе различных явлений – это характерная черта техники, экономики, естествознания. В теории вероятностей это привело к появлению случайных величин. При проведении экспериментов приходится встречаться с переменными величинами, которые принимают различные числовые значения в зависимости от обстоятельств. Примерами таких величин могут служить:
1) результат бросания игрального кубика;
2) число попаданий в цель при 10 выстрелах;
3) остаток вклада по выбранному наугад лицевому счету;
4) продолжительность обслуживания покупателя.
Приведенные примеры, взятые из различных областей, объединяет одно общее положение: результат наблюдения за исходами опыта представляет собой переменную величину, которая под влиянием случайных обстоятельств принимает то или иное числовое значение из некоторого множества. Итак, сформулируем определение случайной величины.
Случайной называется величина, принимающая в результате испытания то или иное (но только одно) возможное значение в зависимости от обстоятельств.
Дискретной называется случайная величина, принимающая конечное число значений.
Пример.
Бросают игральный кубик. Случайная величина – выпадение какого-либо количества очков. Случайная величина может принять значения 1, 2, 3, 4, 5, 6.
Случайные величины будем обозначать большими буквами латинского алфавита (X,…), а их значения – соответствующими малыми буквами с индексами или без индексов (x1, x2,…). Вероятности этих значений обозначим через p, т.е. P(X=x1) = p1, …, P(X=xn) = pn.
Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения может быть записан в виде таблицы или функции.
Таблица или ряд распределения выглядит следующим образом
| X | x1 | … | xn |
| P | p1 | … | pn |
Наиболее общей формой задания закона распределения является функция распределения.
Функцией распределения F(x) случайной величины X называется функция, определенная на множестве всех действительных чисел и задающая вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X < x).
1. Функция распределения есть неотрицательная величина, заключенная между нулем и единицей, т.е. 0 ≤ F(x) ≤ 1.
2. Вероятность попадания случайной величины в интервал [ α, β) равна разности значений функции распределения на концах этого интервала, т.е. P(α≤X<β) = F(β) – F(α).
3. Функция распределения есть неубывающая функция, т.е. если β > α, то F(β) ≥ F(α).
4. F (+∞) = 0; F (– ∞) = 1.
