Каждой числовой характеристике случайной величины Х соответствует ее статистическая аналогия. Для математического ожидания случайной величины аналогией является среднее арифметическое наблюденных значений случайной величины:
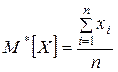
где xi– значение случайной величины, наблюденное в i–м опыте, n– число опытов.
Эта характеристика называется статистическим средним случайной величины.
Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При достаточно большом n статистическое среднее может быть принято приближенно математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.
Подобные статистические аналогии существуют для всех числовых характеристик. Будем обозначать эти статистические аналогои теми же буквами, что и соответствующие числовые характеристики, но снабжать их значком *.
Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины 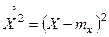 :
:
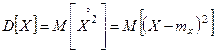
Если в этом выражении заменить математическое ожидание его статистической аналогией – средним арифметическим, мы получим статистическую дисперсию случайной величины Х:

где mx*=M*[X]– статистическое среднее.
Аналогично определяются статистические начальные и центральные моменты любых порядков:
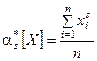
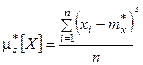
Все эти определения полностью аналогичны определениям числовых характеристик случайной величины. С той разницей, что в них везде вместо математического ожидания фигурирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном n могут быть приняты приближенно равными им.
Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были выведены для математических моментов. В частности, статистический первый центральный момент всегда равен нулю:
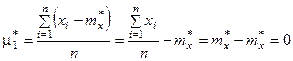
Соотношения между центральными и начальными моментами также сохраняются:
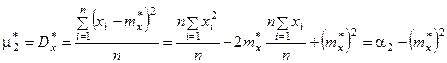
При очень большом количестве опытов вычисление характеристик по приведенным выше формулам становится чрезмерно громоздким. Можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характеристики будут выражаться приближенными формулами:
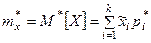
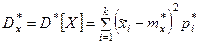
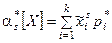
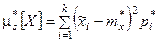
где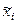 – «представитель» i-го разряда, pi*– частота i–го разряда, k – число разрядов.
– «представитель» i-го разряда, pi*– частота i–го разряда, k – число разрядов.
Как видно, эти формулы полностью аналогичны формулам, определяющим математическое ожидание, дисперсию, начальные и центральные моменты дискретной случайной величины Х, с той только разницей, что вместо вероятностей в них стоят частоты, вместо математического ожидания – статистическое среднее, вместо числа возможных значений случайной величины – число разрядов.
 2014-02-12
2014-02-12 1435
1435