2014-02-12
1261
Этот критерий применяется для проверки простой гипотезы Н 0 о том, что независимые одинаково распределенные случайные величины Х 1, Х 2, …, Хп имеют заданную непрерыв-ную функцию распределения F (x).
Найдем функцию эмпирического распределения Fn (x) и будем искать границы двусторон-ней критической области, определяемой условием
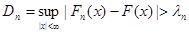. (20.3)
А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н 0 распределение статистики Dn не зависит от функции F (x), и при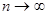 
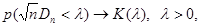
где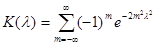 
- (20.4)
- критерий Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λп (α) вычисляется по заданному уровню значимости α как корень уравнения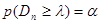 
.
Можно показать, что приближенное значение вычисляется по формуле
,
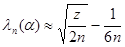где z – корень уравнения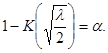 
На практике для вычисления значения статистики Dn используется то, что
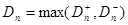, где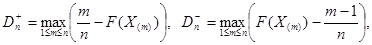 
а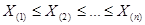 
- вариационный ряд, построенный по выборке Х 1, Х 2, …, Хп.
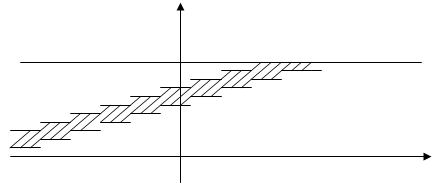
Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости О ху графики функций Fn (x), Fn (x) ±λ n (α) (рис. 1), то гипотеза Н 0 верна, если график функции F (x) не выходит за пределы области, лежащей между графиками функций Fn (x) -λ n (α) и Fn (x) +λ n (α).
|
|
|
х
