Решение. В данном примере число исходных уровней четное, условный отчет (t) в решении произведем следующим образом: Год t

В данном примере число исходных уровней четное, условный отчет (t) в решении произведем следующим образом:

Год
t	-5	-3	-1	+1	+3	+5

Далее произведем расчет необходимых значений, построив вспомогательную таблицу.

Таблица 1

Год	Эмпирические уровни ряда (yi)	Условное обозначение времени (t)	t2	yi*t	Теоретический уровень ряда ()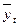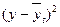
	6,1	-5		-30,5	6,03
	6,3	-3		-18,5	6,52	0,048
	7,1	-1		-7,1	7,01	0,008
	7,6	+1		7,6	7,49	0,012
	8,0	+3			7,98	0,001
	8,4	+5			8,47	0,005
Итого	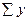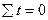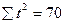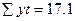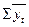= 43,5				= 43,5	0,074

Определим параметры:

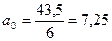млн руб.

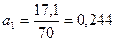млн руб.

Уравнение прямой, представляющие трендовую модель искомой функции, будет иметь вид:

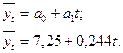Подставляя в уравнение принятые обозначения (t), вычисляем выровненные теоретические значения ():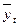

2006г.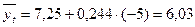

2007г. 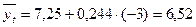и т.д.

Правильность расчета уровней выравниваемого ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда должна быть близка или совпадать с сумой вычисленных уровней выравниваемого ряда, т.е. 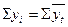.После

Решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.

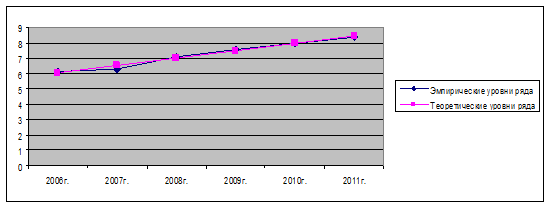
Если число уровней ряда нечетное, то условное обозначение показателя времени примет следующий вид:

Годы
t	-2	-1

Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции.

Экстраполируя при t =7, находим уровень 2012 года.

Точечный прогноз на 2012г.:

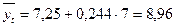млн руб.

Рассчитаем интервальный прогноз объема продажи на 2012г. с вероятностью 0,99.

Интервальный прогноз объёма продажи на 2012г.:

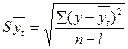где l – число параметров в уравнении тренда;

п – число уровней ряда;

t – коэффициент доверия по распределению Стьюдента при уровне значимости ;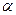

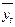− точечный прогноз, рассчитанный по модели.

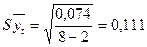млн руб.

Интервальный прогноз объёма продажи на 2012 г.:

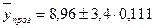
При вероятности р = 0,99 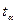= 3,4

8,58 млн руб. < 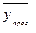< 9,33 млн руб.