Возможным вариантом решения аналитических задач в условиях ограниченности базы исходной статистической информации или при новизне постановки этих задач является применение эвристических методов экономического анализа. Эвристика – это наука о творческом мышлении, а отсюда название группы психологических приемов экономического анализа, классификация которых наглядно представлена на рис. 6.1.
Эвристические методы – это неформализованные методы решения аналитических задач, связанные с опросом и экспертными оценками специалистов и аналитиков, высказывающих свое мнение на основе имеющегося опыта и профессиональных знаний, с последующей математической обработкой полученных мнений для нахождения правильного решения.
Наибольшее распространение из всех эвристических методов получил экспертный метод, предполагающий использование суждений компетентных специалистов[4].
Методы экспертных оценок подразделяются на две группы: индивидуальные и групповые. Эти группы взаимосвязаны между собой, поскольку групповая экспертная оценка формируется на основе первых.
Под методом индивидуальной экспертной оценки понимается процедура получения от каждого из экспертов информации в качественном или количественном виде и ее последующая обработка (аналитиком) с целью представления в заранее предусмотренном виде.

Рис. 6.1 Классификация эвристических методов экономического анализа
Формирование экспертом требуемой от него информации осуществляется в результате интуитивно-логического анализа задачи, в ходе которого каждый из экспертов не только моделирует, но и производит сравнительный анализ альтернатив решения. Таким образом, задача эксперта состоит в том, чтобы разместить сопоставляемые альтернативы (экономические показатели или другие объекты экспертизы) в определенной последовательности, исходя из их экономической значимости, а дальнейшая обработка полученной информации – это задача аналитика. Для получения суждений специалистов используются различные процедуры проведения экспертиз: заочный опрос, дискуссия, интервью.
Заочный опрос проводится путем вручения или пересылки эксперту анкеты. Этот метод достаточно прост, однако ему характерна невысокая надежность получаемых данных по причине возможности неточного понимания экспертом некоторых вопросов. Кроме того, часть элементов изучаемого явления вообще может быть оставлена экспертом без внимания.
Метод дискуссий позволяет согласовать мнения экспертов, но он также не лишен недостатков. Как показывает опыт, на выработку компромиссного суждения оказывает влияние целый ряд психологических факторов: давление мнений большинства, служебный и профессиональный авторитет одного из экспертов, нежелание пересмотреть ранее высказанное мнение и др.
Метод интервью, исключающий недостатки, характерные для первых двух, требует больших затрат времени. Однако и этот метод не исключает искажения полученных суждений в результате психологического воздействия на эксперта (лица, проводящего интервью).
К числу индивидуальных методов получения индивидуальной экспертной оценки относится метод ранговой корреляции (или балльный метод), метод последовательного сопоставления, метод полного факторного эксперимента и метод парных приоритетов.
В основе метода ранговой корреляции заложено ранжирование показателей по степени их влияния на комплексный или результативный[5]. Это делается с помощью баллов, изменяющихся в определенном интервале. Далее числовое значение балла (li) умножают на величину соответствующего частного показателя (Хi) и суммируют эти произведения по n –му набору частных показателей. В формализованном виде эта процедура выглядит следующим образом:

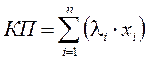 .
.
Достоинство метода: простота формирования и обработки исходной информации; недостаток: трудность ранжирования большого числа объектов.
Уточнение значимости частных оценочных коэффициентов в ранжированном ряду возможно с помощью метода последовательного сопоставления, при котором каждый из коэффициентов оценивается в соотношении с остальными. Совокупность частных показателей оценивается количественно как единое целое числом 100 или 1. На первом этапе каждый частный показатель сравнивается с эталоном, за который принимается средний количественный уровень одного показателя при условии, что все составляющие систему показатели равнозначны. В зависимости от вероятного отклонения от условного среднего уровня эксперт устанавливает количественно значимость каждого частного показателя. На втором этапе эксперт соотносит последовательно количественную оценку каждого показателя с остальными и уточняет ранее присвоенную значимость, принимая во внимание возможные отклонения от эталона и пропорции различий между показателями. Совокупная оценка всех показателей должна быть равна предельному уровню шкалы – 100 единиц. Таким образом, этот метод позволяет установить не только сам факт различий в значимости, но и количественно соизмерить вероятную величину этих различий.
Сущность следующего метода заключается в построении матрицы полного факторного эксперимента и оценки экспертом ситуаций, обусловленных показателями матрицы[6].
Матрица полного факторного эксперимента представляет собой таблицу, содержащую N -ое число ситуаций (экспериментов), равное 2 n, где n – число частных оценочных показателей (факторов): N = 2 n.
Показателями матрицы являются положительные или отрицательные значения факторов, установленные в определенной последовательности с учетом того, что сумма наблюдаемых значений по каждому i -му фактору была равна 0. Только в этом случае обеспечивается получение независимых значений слагаемых уравнения регрессии, которые характеризуют свободное от субъективизма влияние каждого из частных показателей на комплексный.
Матрица полного факторного эксперимента строится по форме табл. 6.4, в которой рассмотрен условный пример:
X 1,2,3 –частные оценочные показатели;
Y – индивидуальная экспертная оценка ситуации, отраженной в матрице, присвоенная с помощью шкалы отношений от 10 до 100.
Знак (+) соответствует наибольшему количественному выражению фактора; знак (-) – минимальному значению, независимо от фактического абсолютного уровня отдельного оценочного показателя.
Таблица 6.4
Макет матрицы полного факторного эксперимента (при n =3)
| Число наблюдений | Число факторов (n=3) | Yср | ||
| X1 | X2 | X3 | ||
| + | + | + | ||
| - | + | + | ||
| + | - | + | ||
| - | - | + | ||
| + | + | - | ||
| - | + | - | ||
| + | - | - | ||
| - | - | - |
При обработке результатов ставится задача нахождения коэффициентов регрессии лi в уравнении
Y = ∑ л i · Чi,
где i = 1…3.
Коэффициент регрессии лi находим по формуле
л i = аi / ∑ аi,
где аi – количественное выражение исследуемого фактора, алгоритм которого представлен формулой
аi = (∑ в ij · Х.i) / N,
где N = 1...8; вij – условное число, соответствующее наибольшему или наименьшему уровню фактора. Для упрощения расчетов в качестве основания принята единица (+1;-1).
В приведенном примере
а1 = (100-80+70-40+75-35+20-10)/8=12,5;
а2 =(100+80-70-40+75+35-20-10)/8=18,75;
а3 =(100+80+70+40-75-35-20-10)/8=18,75.
∑аi = 12,5+18,75+18,75=50.
Находим л1, л2, л3: л1 =12,5/50 = 0,25; л2,3 = 18,75/50 = 0,375.
После проведенных вычислений решение уравнения регрессии выглядит следующим образом:
Y = 0,25· Х1 + 0,375· Х2 + 0,375· Х3
Метод парных приоритетов: его суть заключается в установлении значимости объектов в совокупности, путем последовательного попарного сравнения между собой с целью выявления приоритетных отношений и количественного измерения величины предпочтений. Процедура реализации исследуемого метода состоит из нескольких последовательных операций[7]:
1. Эксперты высказывают свои суждения, применяя метод парных сравнений, однако предварительно не дают предпочтения в парах числовых выражений. Для облегчения процедуры строится квадратная матрица в виде таблицы шахматной формы. Ее подлежащее обозначено условно i, а реквизиты сказуемого – j. Массив объектов (i) представляет собой частные оценочные показатели (Х1, Х2, Х3,…Хn). В массиве j перечисляются те же объекты в той же последовательности (Х1, Х2, Х3,…Хn).
В матрице приоритетным массивом является i по отношению к j, отсюда объекты из массива i последовательно сравниваются с объектами из массива j. Каждой сопоставляемой паре показателей (ситуаций) присваивается одна из пяти символических качественных характеристик, выражающих возможные предпочтения разной величины одного фактора над другими:
– больше (всегда строго больше) – «>»,
– не меньше (больше, но может быть равно) – «≥»,
– равно – «=»,
– меньше (всегда строго меньше) – «<»,
– не больше (меньше, но может быть равно) – «≤».
На пересечении строки i –го массива с графой j -го массива эксперт ставит знак количественной оценки предпочтения, соответствующей своему взгляду (см., например, табл. 6. 5).
Таблица 6.5
Матрица расстановки парных приоритетов (строится по каждому эксперту в отдельности)
| Массив i (Хn) | Массив j (Хn) | ||||
| Х1 | Х2 | Х3 | Х4 | Х5 | |
| Х1 | = | > | > | ≥ | ≥ |
| Х2 | < | = | ≥ | ≤ | < |
| Х3 | < | ≤ | = | ≤ | < |
| Х4 | ≤ | ≥ | ≥ | = | ≤ |
| Х5 | ≤ | > | > | ≥ | = |
2. После того как матрица составлена, эксперт на основе своего профессионального опыта и имеющейся информации о содержании и значении объекта в системе оценивает отношение наиболее важного частного показателя к наименее важному в системе. Другими словами, экспертом задаются пределы степени значимости в оцениваемых объектах. На этом действия высказывания мнений экспертами заканчивается, и далее следуют операции, связанные с вычислениями числовых значений приоритетов и установления удельных весов важности показателей.
3. С целью перевода качественных символических оценок в числовые значения составляется матрица переменных величин аij (массив А), представляющих собой числовое выражение символов предпочтения (табл. 6.6). Для этого результаты количественных символических оценок представим следующей системой парных сравнений:
Х1=Х1; Х1>Х2; Х1>Х3; Х1≥Х4; Х1≥Х5;
Х2<Х1; Х2=Х2; Х2≥Х3; Х2≤Х4; Х2<Х5;
Х3<Х1; Х3≤Х2; Х3=Х3; Х3≤Х3; Х3<Х5;
Х4≤Х1; Х4≥Х2; Х4≥Х3; Х4=Х4; Х4≤Х5;
Х4≤Х1; Х5>Х2; Х5>Х3 Х4≥Х5; Х5=Х5.
Таблица 6.6
Квадратная матрица переменных коэффициентов аij (массив А)
| Массив i (Хn) | Массив j (Хn) | ||||||
| Х1 | Х2 | Х3 | Х4 | …. | Хj | Хn | |
| Х1 | а11 | а12 | а13 | а14 | …. | а1j | а1n |
| Х2 | а21 | а22 | а23 | а24 | …. | а2j | а2n |
| Х3 | а31 | а32 | а33 | а34 | …. | а3j | а3n |
| Х4 | а41 | а42 | а43 | а44 | …. | а4j | а4n |
| …. | …. | …. | …. | …. | …. | …. | …. |
| Хi | аi1 | аi2 | аi3 | аi4 | …. | аij | аin |
| Хn | аn1 | аn2 | аn3 | аn4 | …. | аnj | аnn |
4. На основании индивидуальных экспертных оценок отношения объекта с максимальной значимостью к объекту с минимальной значимостью в системе находится среднее соотношение между ними (ŋ.) по формуле средней арифметической:
ŋ. = (∑ ŋm) / m; ŋ m = хi max / хi min,
где m – количество экспертов; ŋ m – соотношение между объектами, которые обладают крайними уровнями значимости в системе, по данным индивидуальной оценки.
5. Далее строится квадратная матрица смежности, которая заполняется числовыми значениями переменных величин аij. По системе парных сравнений подбираются соответствующие коэффициенты аij, принимая во внимание следующее равенство:
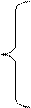 1+y при Хi>Хj;
1+y при Хi>Хj;
1+0,5·у при Хi≥Х;
аij = 1 при Хi = Хj;
1-y при Хi<Хj;
1-0,5·у при Хi≤Хj,
где y – величина, характеризующая диапазон изменения влияния частных оценочных показателей на комплексный.
Величина y определяется на основе среднего коэффициента по формуле:
y = [ (ŋ – 1) / (ŋ + 1) ] · [ (n + 1) / n ],
где n – число объектов Хi.
6. Чтобы установить степень влияния каждого исследуемого объекта (фактора), проводится расчет значений приоритетов итеративным методом. В общем виде итерация – это определенный этап серии процедур, в ходе которого получают решение, но с учетом предыдущего, по тому же алгоритму и с использованием той же зависимости.
На каждой последующей итерации степень влияния каждого частного коэффициента на комплексный показатель уточняется. Согласно теореме Перрона-Фробениуса, при числе итераций, стремящемся к бесконечности (t →∞), значимость исследуемого объекта в системе достигает своего истинного уровня[8].
Итерированная «сила» первого порядка объекта Хi обозначается Рi (1) и находится как сумма влияний данного показателя без учета степени влияния других показателей, составляющих систему
Рi (1) = ∑ аij.
При этом влияние каждого показателя распределяется согласно вектору:
Р (1) = [ Р1(1), Р (1),…Рi (1)…,Рn (1) ].
Используя предыдущую формулу и матрицу А, вектор сил объектов можно изобразить в виде алгоритма
Р (1)= ∑ [ ∑ аij ∑ а2j …, ∑ аnj ].
При второй итерации в качестве силы объекта принимается итерированная сила первого порядка. Расчет итерированной силы второго порядка по каждому показателю ведется с учетом влияния других показателей по формуле
Рi (2)=Рi (1)·л i (1) или Рi (2)= ∑ аij ·л i (1).
Все последующие итерации проводятся в аналогичном порядке:
Р(t)= л Р (t -1),
где t – порядковый номер итерации.
Таким образом, процедура расчета заключается в последовательном преобразовании векторов согласно матрице А путем итераций.
Уровень значимости каждого i -го объекта (л i (1)) по t -й итерации определяется путем расчета нормированной итерированной силы t -го порядка i -го показателя по формуле
л it = (∑ аij) / (∑∑ аij),
где л it – значимость i -го показателя по t -й итерации, полученная в результате нормирования.
При этом сумма значимостей всех показателей по каждой итерации должна быть равна 1,0: ∑л i = 1,0.
Однако приведенный алгоритм может применяться только после первой итерации t (1), когда не учитываются итерированные силы (влияния) других частных оценочных показателей (объектов).
Процесс расчета нормированной силы (значимости) каждого объекта в системе с учетом влияния других компонентов обобщенно можно представить в виде алгоритма:
лi t = (∑(аij · л I t-1)) / (∑∑(аij л it-1)),
где л it-1 – значимость i -го показателя после предыдущей итерации, так как в расчете по следующей t -й итерации в основу принимаются значения по предыдущей (t-1)-й итерации.
Обобщая характеристику индивидуальных методов экспертных оценок, следует отметить, что в ряде научных исследований, проводимых, в частности, на кафедре экономического анализа и статистики ГОУ ВПО КГТЭИ, была реализована их сравнительная оценка, в ходе которой выбор наиболее эффективной модели экспертных оценок осуществлялся, исходя из системы критериев, предъявляемых к каждому из методов. Главным образом это: транзитивность исходной информации и приоритетных отношений между частными показателями в системе (т. е. логическая их зависимость); доступность и простота представления объекта при высказывании суждений экспертами; достаточное ощущение экспертами интервалов между объектами, возможность их количественного выражения с помощью определенной шкалы измерений; наибольшая чувствительность метода к различиям в значимости оцениваемых показателей, наибольшая точность количественного выражения приоритетных отношений и согласованность экспертов. Последние три критерия являются критериями оценки качества экспертного решения (см. табл. 6.7).
Обобщение итогов исследования привело к выводу о преимущественной целесообразности применения в практике аналитических исследований метода расстановки парных приоритетов, сущность которого схематически изображена на рис. 6.2. Обратим внимание на основные достоинства этого метода, выявленные в процессе исследования:
– путем парных сравнений эксперту значительно проще реализовать процедуру высказывания суждений, когда не требуется одновременного сравнения между собой нескольких объектов, а самое главное – непосредственной оценки их приоритетных отношений;
– этот метод единственный, по сравнению с другими моделями, не требует от эксперта строгой транзитивности в момент высказывания суждений, что особенно важно при многокритериальной оценке разнохарактерных и взаимосвязанных сторон деятельности предприятий. Предполагая не транзитивность парных сопоставлений, т. е. нарушение логичности приоритетных зависимостей между частными показателями, эксперт проводит сопоставление независимо от результатов предыдущих сравнений, и тем самым ослабляется влияние ранее допущенной ошибки на результаты оценки, что совершенно исключается в процедурах других методов;
– метод парных сравнений, используемый экспертами при высказывании мнений, позволяет полнее реализовать их возможности и не требует высокой квалификации, так как упрощается сама процедура высказывания суждений в связи с сопоставлением только двух объектов без непосредственного числового выражения приоритетов;
 2014-02-12
2014-02-12 2753
2753
