Расчет по данным, характеризующим начало участка

Известны мощность и напряжение в начале участка S ₁ и 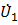; требуется определить мощность и напряжение в конце участка S ₂ и 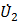. На практике этот случай имеет место тогда, когда возникает необходимость передачи заданной мощности источника (электростанции), при фиксированном напряжении на его шинах, в приемную систему или узел потребления. При этом следует определить, каковы будут затраты (потери) мощности и напряжения на приемном конце электропередачи. Полагаем, что нагрузка имеет активно-индуктивный характер (ток звена 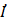отстает от напряжения 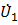на угол 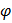). Тогда комплексное значение полной мощности в начале участка будет

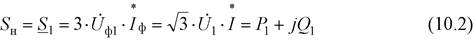Откуда комплексное значение полного тока

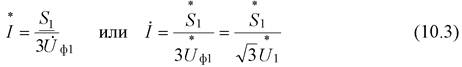и значения его составляющих

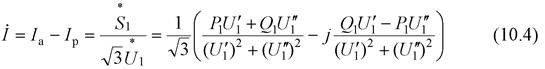вычисляют точно через известные мощность S ₁ и напряжение 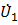в начальном узле схемы. По этой же причине имеется возможность точно вычислить зависящие от тока потери мощности ΔS и падение напряжения Δ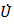а потому расчет режима участка выполняется в один этап от начала к концу звена, т. е. реализуется прямая (точная) процедура расчета.

Коэффициент мощности в начале ветви

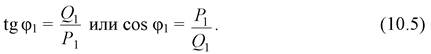
Предположим, что известно напряжение 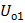(его замер) в начале звена. Тогда при известной мощности S ₁ можно точно определить ток ветви в виде

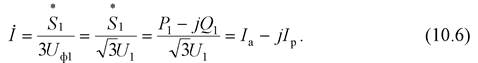При протекании тока 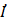по участку с сопротивлением Z происходит потеря активной и реактивной мощности, которые в соответствии с законом Джоуля – Ленца запишем через составляющие тока:

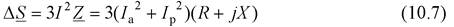или, пользуясь значениями активной и реактивной мощности, в соответствии

с (10.6) запишем

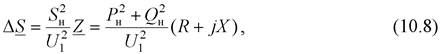откуда потери активной и реактивной мощности

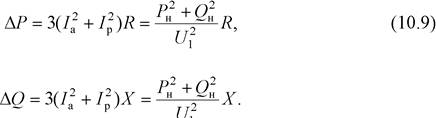Множитель 3 исчез, поскольку выполнена подстановка модуля тока, вычисленного через линейное напряжение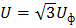

Поток мощности в конце ветви меньше на величину потерь:

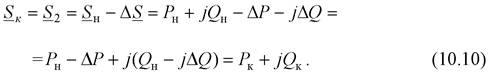Ток в продольном участке сети наряду с потерями мощности вызывает

падение напряжения

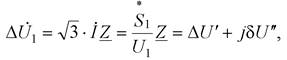на величину которого (в соответствии с указанным направлением тока) напряжение в конце участка меньше напряжения в начале

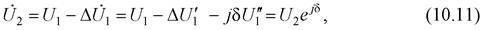где модуль и фаза напряжения приемного конца электропередачи определяются по формулам (9.24) и (9.26). Составляющие вектора падения напряжения Δ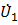можно найти по выражениям, использующим ток (9.33) или мощность начала участка (9.28).

Режим напряжения данного участка сети можно характеризовать с помощью векторной диаграммы (рис. 10.2), построенной в координатных осях +, j.

С учетом найденного напряжения 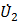мощность в конце звена (10.10) можно также записать в вид

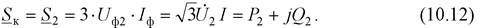Откуда с учетом (10.3) получим очень важное выражение для тока звена

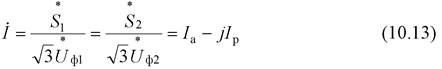или в записи через линейные напряжения (с учетом отмеченного допущения)

имеем

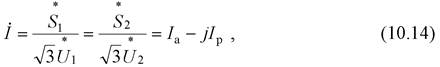т. е. ток можно вычислить по данным начала или конца звена.

Таким образом, ток участка сети можно вычислить через мощность и напряжение в начале или конце звена.

Рабочий режим участка сети можно характеризовать распределением полной мощности по участку (рис. 10.1) и соответствующей векторной диаграммой (рис.10.2), отражающей связь мощностей начала, конца участка и потерь в нем посредством балансового соотношения (10.10).

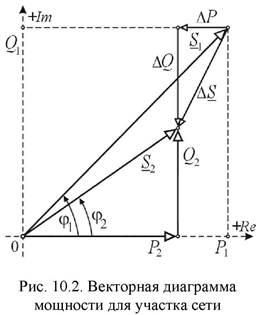В соответствии с (10.10) из исходного вектора мощности начала участка, откладывая параллельно оси абсцисс, вычитаем вектор потерь активной мощности ΔP. С конца вектора ΔP, откладывая параллельно оси ординат, вычитаем вектор потерь реактивной мощности ΔQ. В итоге полученный вектор Δ S вычитаем из вектора S₁. Соединив конец вектора Δ S с началом координат, получим вектор мощности S ₂ в конце участка с составляющими P₂ и Q₂ (рис. 10.2). Углы наклона 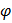₁ и 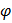₂ векторов мощности S ₁ и S ₂ к оси вещественных величин определяют значения коэффициента мощности. В частности, в конце участка имеем

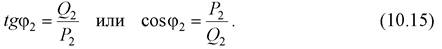Коэффициент полезного действия участка сети в процентах

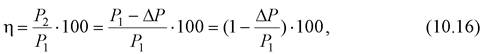т. е. снижение потерь активной мощности увеличивает КПД электрической

сети.