Определители и их свойства. Обратная матрица. Ранг матрицы

 

Понятие определителя возникло в связи с задачей решения систем линейных уравнений.

Определитель матрицы А = (а _{i j}) есть некоторое число, равное алгебраической сумме из n! произведений, построенных из элементов матрицы по определенным правилам.

 

Обозначение: определитель матрицы А обозначается следующим образом

 

= Δ.

 

Рассмотрим определители 2-го и 3- го порядков.

 

Определение 15. Определителем 2-го порядка, соответствующим

квадратной матрице А = , называется число

равное а ₁₁ а ₂₂ – а ₂₁ а ₁₂.

 

Определение 16. Определителем 3-го порядка, соответствующим

квадратной матрице 3-го порядка А =

называется число, равное

 

а ₁₁ 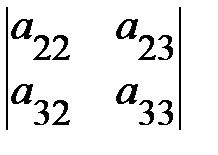- а ₁₂ + а ₁₃

 

Такой способ вычисления определителя называется «разложением определителя по первой строке».

В дополнение к этому для вычисления определителя третьего порядка можно воспользоваться также «правилом треугольников», которое символически записывается следующим образом

 

 

Пример 9. Вычислить .

Решение. Способ 1 – методом «разложения по первой строке»:

 

 

Способ 2 – по «правилу треугольников»:

 

½ А ½= 1(-1)3 + 3(-3)(-1) + 2×2(-2) – (-1)(-2)(-1) – 2×3(-3) - 1×2×3 =

= -3 + 9 -8 + 2 + 18 - 6 = 12.

 

Общим методом вычисления определителей 3-го и более высоких порядков является метод разложения определителя по любой строке или по любому столбцу. Для этого требуется ввести новые понятия.

 

Определение 17. Минором к-го порядка произвольной матрицы А

называется определитель, составленный из элементов

матрицы, расположенных на пересечении каких-либо k строк и

k столбцов.

 

Для матрицы А = можно указать, например, такие миноры 2- го порядка: 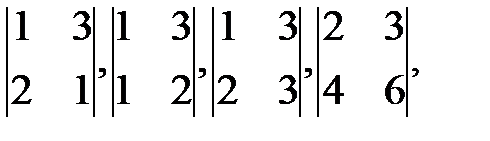и т. д., и миноры 3- го порядка:

 

, , и .

 

Миноров более высокого порядка у матрицы нет.

 

Определение 18. Минором М _{i j} к элементу а _{i j} определителя квадратной

матрицы А называется определитель, полученный из

данного вычеркиванием i -й строки и j -го столбца.

 

Для матрицы А = минор М_{3 2} равен М_{3 2} = .

 

Определение 19. Алгебраическим дополнением А _{i j} к элементу а _{i j}

квадратной матрицы А называется число

А _{i j} = .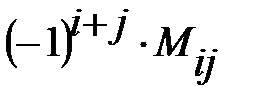

Пример 10. Найти А _{2 3} для матрицы из примера 9:

Решение. А _{2 3} = (-1) ³⁺² М _{3 2} = (-1)× (-6) = 6.

 

Пример 11. Вычислить определитель detA = 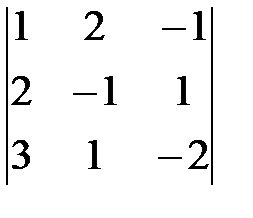, разложив его:

а) по элементам второй строки; б) по элементам первого столбца.

Решение:

а) detA = 2(-1)²⁺¹× (-1)(-1) ²⁺²× + 1× (-1) ²⁺³× =

= 6 –1 + 5 = 10.

 

б) detA = 1(-1) ¹⁺¹ 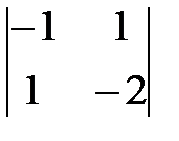+ 2(-1)²⁺¹ + 3(-1) ³⁺¹ =

= 1 + 6 + 3 = 10.

 

При вычислении определителей полезно знать свойства определителей. Это позволит упростить вычисление определителя.

 

Свойства определителей

 

1. Определитель квадратной матрицы А не меняется при ее

транспонировании:

det A = det A^т.

2. При перестановке местами каких- либо двух строк (или столбцов)

определитель сохраняет абсолютную величину, но меняет знак на противоположный.

3. Определитель квадратной матрицы, имеющей две одинаковые сроки (или столбца), равен нулю.

4. Умножение всех элементов некоторой строки (или столбца) определителя

на число l равносильно умножению определителя на это число l.

5. Если элементы некоторой строки (или столбца) равны нулю, то определитель равен нулю.

6. Если к элементам некоторой строки (или столбца) определителя прибавить соответствующие элементы какой-либо другой строки (или столбца), умноженные на произвольное число l, то величина определителя не изменится.

7. Если элементы каких-либо двух строк (или столбцов) определителя пропорциональны или равны, то определитель равен нулю.

 

Пример 12. Вычислить определитель det A = , сведя его вычисление к вычислению одного определителя 2-го порядка.

Решение. 1) используя свойство 6, прибавим к элементам первого столбца соответствующие элементы третьего столбца. Получим определитель ;

2) к элементам второго столбца прибавим соответствующие элементы третьего столбца, умноженные на 2, в итоге получим определитель , который

легко вычисляется разложением по первой строке

det A = (-1)(-1) ¹⁺³ 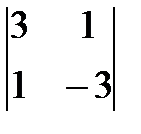= - (-9 – 1) = 10.

 

Обратная матрица

 

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной в противном случае.

Каждая невырожденная матрица А имеет единственную обратную матрицу А ^-1 такую, что

А ^{- 1}×А = А× А^{- 1} = Е.

Составим матрицу А^*, элементами которой являются алгебраические дополнения А _{i j}:

А ^* = .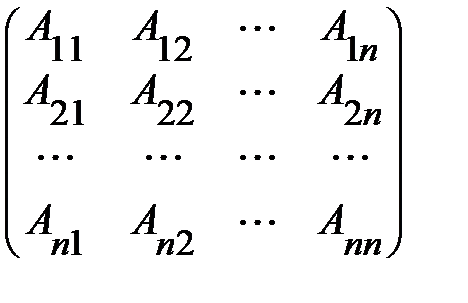

 

Матрица (А ^*) ^Т называется присоединенной матрицей:

 

(А ^*) ^Т =

 

 

Обратная матрица А^-1 вычисляется по формуле

 

А ^-1 = .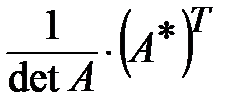

Пример 13. Вычислить обратную матрицу к матрице .

Решение. Составим присоединенную матрицу (А ^*) ^Т, а для этого вычислим алгебраические дополнения ко всем элементам матрицы А:

А ₁₁ = (-1) ¹⁺¹ ; А _{1 2} = (-1) ¹⁺² = - 7; А _{1 3}= (-1) ¹⁺³ ;

А _{2 1}= 3; А _{2 2}= 1; А_{2 3}= 5; А _{3 1}= 1; А _{3 2}= -3; А _{3 3} = -5;

Запишем (А^*) ^Т =

Определитель матрицы А был вычислен ранее и равен det A = 10. Тогда обратная матрица будет

А ^-1 = =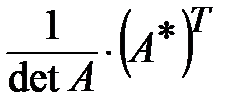

Определители двух взаимно обратных матриц являются взаимно обратными числами

det A ×det A ^-1 = 1.

 

 

Ранг матрицы

 

Пусть задана матрица А размером m´n, где m – число строк, а n – число столбцов матрицы, и пусть m< n. Если в этой матрице выделить какие-либо k cтрок и k столбцов (k £ m), то тем самым получим минор М k – го порядка.

 

Определение 20. Рангом матрицы А (обозначается r (A)) называется

наивысший порядок k отличных от нуля миноров.

 

Ранг нулевой матрицы по определению равен нулю.