Рис. 8.3 Представление сложной функции ступенчатой функцией.
В этом случае реакция цепи определяется при помощи интеграла Дюамеля.
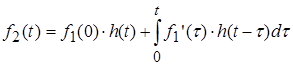 (8.5)
(8.5)
Если известна или легко определяется импульсная характеристика цепи, то сложное воздействие f1(t) аппроксимируется последовательностью прямоугольных импульсов (рис. 8.4)
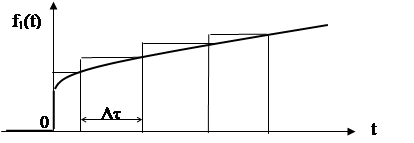 |
Рис. 8.4. Представление сложной функции последовательностью прямоугольных импульсов.
В этом случае реакция цепи f2(t) определяется при помощи интеграла наложения.
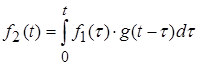 . (8.6)
. (8.6)
Расчёт ЭЦ временным методом производится в следующем порядке:
1. Определение переходной h(t) или импульсной g(t) характеристики цепи.
2. Определение переходной h(t-t) или импульсной g(t-t) характеристики путём замены t на t-t.
3. Определение производной от входного напряжения u1(t) по времени.
4. Определение реакции с помощью интеграла Дюамеля или наложения.
Пример: Определить u2(t) цепи рис. 8.5.
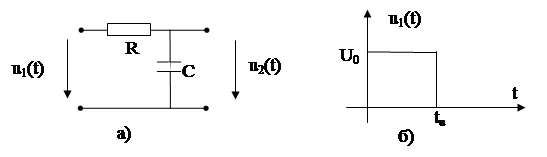 |
Рис. 8.5. Исходная схема а) и вид воздействия б).
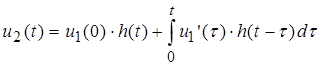 ;
;
u1(0)=U; 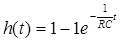 ; u1’(t)=U0’=0;
; u1’(t)=U0’=0;
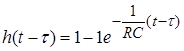
При 0£ t £ tU
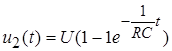 .
.
При t ³ tU
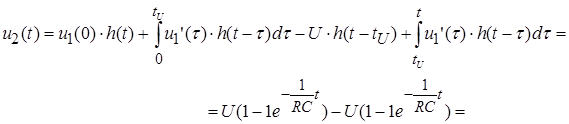
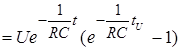 .
.
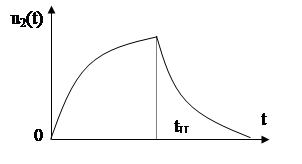 |
Рис. 8.6. Временная зависимость выходного напряжения.
При передаче информации по каналам связи в процессе преобразования сигналов в различных устройствах используют периодические несинусоидальные и непериодические (импульсные) воздействия.
Методы анализа цепей, находящихся под воздействием таких сигналов, базируются на спектральном (частотном) представлении этих сигналов.
Спектральное представление воздействий – это разложение воздействий на сумму гармонических составляющих с различными частотами.
Периодические несинусоидальные воздействия представляются в виде ряда Фурье
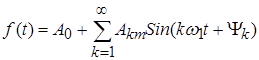 . (8.7)
. (8.7)
Слагаемые ряда Фурье представляют собой гармонические колебания с частотами kw1(k=1,2…). Поэтому периодическое несинусоидальное воздействие – это результат наложения бесконечно большого числа гармонических колебаний с частотами w1, 2w1, 3w1, … с амплитудами А1m, А2m, А3m, … и начальными фазами y1, y2, y3
Совокупность частотных параметров Аkm образует амплитудный спектр АЧС (рис. 8.7, а), yk - фазовый спектр ФЧС (рис. 8.7, б). Спектры периодических несинусоидальных воздействий – дискретные (линейчатые).
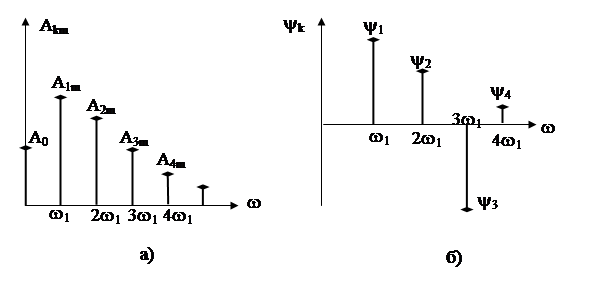 |
Рис. 8.7. Амплитудный а) и фазовый б) спектры периодических несинусоидальных сигналов.
Непериодические воздействия могут быть представлены в виде наложения гармонических составляющих с помощью интеграла Фурье
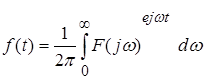 , (8.8)
, (8.8)
где 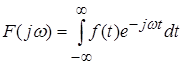 .
.
С помощью интеграла Фурье непериодические воздействия представляются как результат наложения бесконечно большого числа бесконечно близких по частоте гармонических колебаний с бесконечно малыми амплитудами.
Функцию F(jw)=F(w)ejj(w) называют спектром непериодическоговоздействия, F(w) - спектральной плотностью амплитуд (амплитудный спектр) (рис. 8.8а), j(w) - спектром фаз (рис. 8.8б)
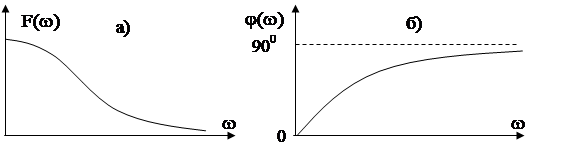 |
Рис. 8.8. Пример амплитудного а) и фазового б, спектров непериодического сигнала.
Представление периодических несинусоидальных и непериодических воздействий в виде суммы гармонических колебаний позволяет применять к спектрам все методы расчёта установившихся синусоидальных процессов в ЛЭЦ.
В основе частотного метода анализа ЛЭЦ лежит использование свойств комплексного коэффициента передачи цепи. Расчёт ведётся в следующем порядке:
1. Определяем спектр воздействия
2. Определяется комплексная передаточная функция цепи H(jw)
3. Определяется спектр реакции
4. По найденному спектру определяется оригинал реакции.
Пример: Определить u2(t) цепи рис. 8.9, а частотным методом
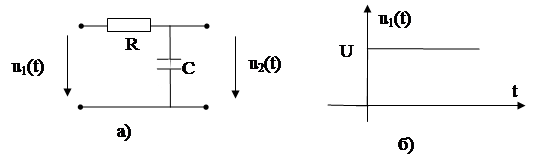 |
Рис. 8.9. Исходная схема а) и вид воздействия б).
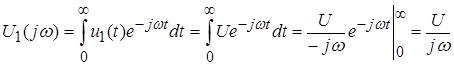 ;
;
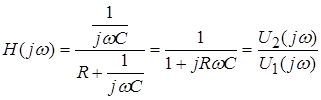 ;
;
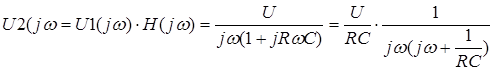 .
.
По таблице «оригинал- изображение» при p=jw находим
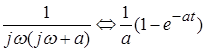 ;
;
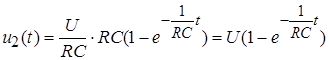 .
.
 2014-02-13
2014-02-13 1431
1431
