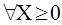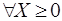Таблица 1.11
Таблица 1.8
| Элементы | Элементы таблицы | |
| Старой | Новой | |
| Разрешающий | ak,s | 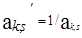 |
| Разрешающей строки | ak,j | 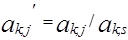 |
| Разрешающего столбца | ai,s | 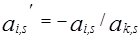 |
| Все остальные | ai,j | 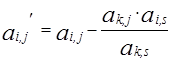 |
В этой таблице введем следующие индексы:
S - индекс элементов разрешающего столбца,
K - индекс элементов разрешающей строки.
|
|
 | |||||
| |||||
| |||||
Суть преобразований симплекс-метода рассмотрим на примере 1.4. Давайте вспомним ограничивающие неравенства и целевую функцию из этого примера и найдем max целевой функции, пользуясь вышеизложенным методом:
F = 908X1 + 676X2 ® max.
 X1 + X2
X1 + X2  14,
14,
X2  10,
10,
10 X1 + 8 X2  120,
120,
7X1 + 5 X2  70,
70,
4X1 + 2X2  28,
28,
|
Преобразуем ее в каноническую форму, вводя дополнительные переменные Xj 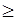 0, и превратив неравенства в равенства. Следует обратить внимание, что если в неравенстве стоит знак "
0, и превратив неравенства в равенства. Следует обратить внимание, что если в неравенстве стоит знак " ", то при свободной переменной пишут " - ", в противном случае - " + ":
", то при свободной переменной пишут " - ", в противном случае - " + ":
 X1 + X2 = 14 - X3,
X1 + X2 = 14 - X3,
X2 = 10 - X4 ,
10 X1 + 8 X2 = 120 - X5 ,
7X1 + 5 X2 = 70 - X6 ,
4X1 + 2X2 = 28 - X7 .
Чтобы приступить к процедуре симплекс-метода, нужно из множества базисных решений полученной системы уравнений сначала найти опорное. С учетом этого в решении задач симплекс-методом различают три этапа:
- нахождение первоначального базисного решения и формирование исходной симплекс-таблицы;
- определение допустимого решения;
- определение оптимального решения.
1-й этап
Первоначальное базисное решение систем находим, полагая свободными переменные X1 и X 2.
 Тогда X3 = 14 - X1 - X2 ,
Тогда X3 = 14 - X1 - X2 ,
X4 = 10 - X2 ,
X5 =120 - 10X1 - 8X2 ,
X6 = 70 - 10X1 - 5X2,
X7 = 28 - 4X1 - 2X2 ,
F = 908X1 + 676X2 = 0.
Преобразуем эти уравнения к нормальному виду:
 X3 = 14 - (X1 + X2 ),
X3 = 14 - (X1 + X2 ),
X4 = 10 - (0X1 + X2 ),
X5 =120 - (10X1 + 8X2 ),
X6 = 70 - (7X1 + 5X2 ),
X7 = 10 - (4X1 + 2X2 ),
F = 0 + 908 X1 + 676 X2 .
Полученную систему уравнений запишем в виде исходной симплекс-таблицы (табл. 1.9). В табл. 1.9 нет отрицательных свободных членов. Следовательно, нами получено опорное (допустимое) решение, так как допустимым решением является любое неотрицательное решение (при котором 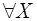 > 0), но оно не является оптимальным.
> 0), но оно не является оптимальным.
Очевидно, что если бы при всех неизвестных в целевой функции F стояли положительные коэффициенты, то было бы достигнуто максимальное значение F. Отсюда вытекает признак оптимальности допустимого решения: в F - строке симплекс-таблицы не должно быть отрицательных коэффициентов.
Таблица 1.9
| Базисные переменные Xб | Свободный член | Свободные переменные | |
| X1 | X2 | ||
| X3 | |||
| X4 | |||
| X5 | |||
| X6 | |||
  X7 X7 | |||
| F | - 908 | - 676 |
2-й этап
Напомним, что основная операция симплекс-метода заключается в том, что некоторая базисная переменная 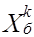 замещается на свободную переменную
замещается на свободную переменную 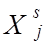 . При этом операция замещения выполняется при соблюдении следующих условий:
. При этом операция замещения выполняется при соблюдении следующих условий:
- значение целевой функции F в новом опорном (допустимом) решении должно быть больше, чем в предыдущем;
- новое решение системы должно быть также опорным (допустимым).
В нашем примере первое условие выполняется, если разрешающий элемент положительный и выбран в столбце отрицательного коэффициента F -строки.
Второе условие выполняется, если разрешающий элемент находится как минимальное положительное отношение элементов столбца свободных членов к соответствующим элементам разрешающего столбца.
По выше изложенному правилу для нахождения допустимого решения меняют местами базисные и свободные переменные. Для этого находят разрешающий элемент (в табл. 1.9 он взят в рамку). В нашем случае разрешающим может быть как столбец X 1, так и X2. Деля свободные переменные на соответствующие значения X1 и X 2 (кроме строки F), находим наименьшее положительное значение. Для столбца X 1:
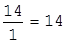 ;
; 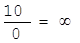 ;
; 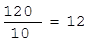 ;
; 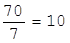 ;
; 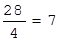 .
.
Для столбца X2:
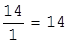 ;
; 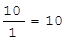 ;
; 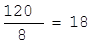 ;
; 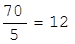 ;
; 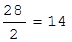 .
.
Наименьшее отношение 28/4 определяет разрешающую строку и разрешающий столбец, а пересечение разрешающего столбца и разрешающей строки - разрешающий элемент aks = 4. В табл. 1.9 разрешающий столбец и разрешающую строку отмечаем стрелками (®). Определив aks , строят следующую таблицу, в которой меняют местами переменные, входящие в строку и столбец разрешающего элемента, т.е. переводят базисные переменные в свободные, а свободные - в базисные.
В нашем примере меняем местами переменные Х 7 и Х 1 , отмеченные в табл. 1.9 стрелками. Коэффициенты новой табл. 1.10 находят по коэффициентам старой табл. 1.9, используя выражения, приведенные в табл. 1.8 и “правило прямоугольника”. В табл. 1.10 снова не имеем оптимального решения.
 Таблица 1.10
Таблица 1.10
| Базисные переменные Хб | Свободный член В | Свободные переменные | |||||||||||
| X7 | X2 | ||||||||||||
| Х3 | - 1/4 | 1/2 | |||||||||||
  Х4 Х4 | |||||||||||||
| Х5 | -5/2 | ||||||||||||
| Х6 | -7/4 | 3/2 | |||||||||||
| Х1 | 1/4 | 1/2 | |||||||||||
| F | -222 | ||||||||||||
По вышеописанным правилам в табл. 1.10 находим разрешающий элемент 1 и строим новую табл. 1.11 сделав замещение базиса (Х4 и Х2). Особо подчеркнем, что для нахождения разрешающего элемента мы должны выбирать наименьшее положительное значение, т.е. отрицательные отношения свободных членов к коэффициентам разрешающего столбца мы не рассматриваем.
| Базисные переменные Хб | Свободный член В | Свободные переменные | |||||||||||
| X7 | X4 | ||||||||||||
| Х3 | - 1/4 | - ½ | |||||||||||
| Х2 | |||||||||||||
| Х5 | -5/2 | - 3 | |||||||||||
| Х6 | -7/4 | - 3/2 | |||||||||||
| Х1 | 1/4 | - ½ | |||||||||||
| F | |||||||||||||
3-й этап
Проверим, является ли найденное решение оптимальным, а для нашего примера - максимальным. Для этого сделаем анализ целевой функции F: F = 8576 + 227 X7 + 222 X4.
Целевая функция не содержит отрицательных коэффициентов и имеет наибольшее значение в последней таблице, нами получено оптимальное решение:
X3 = 2; X2 = 10; X5 = 20; X6 = 6; X1 = 2; X7 = X4 = 0;
Fmax = 8576.
Обратите внимание, что результаты решения симплекс методом и графическим совпадают.
В соответствии с рассмотренной последовательностью, алгоритм симплекс-метода должен иметь следующие блоки:
1. Нахождения первоначального базисного (опорного) решения и формирование исходной таблицы.
2. Отыскание разрешающего элемента a ks (нахождение отрицательного свободного члена - b i < 0 и минимального отношения b i / aij ; если в строке отрицательного свободного члена нет отрицательных коэффициентов, то задача неразрешима).
3. Перерасчет новой таблицы по формулам табл. 1.8.
4. Проверка наличия отрицательного свободного члена. Если он есть, то переходим к п. 2. Отсутствие отрицательного свободного члена означает, что получено опорное (допустимое) решение.
5. Аналогично п. 2 - 4 выполняется перерасчет таблицы при поиске оптимального решения.
Решение задачи ЛП симплекс-методом в матричной форме
Требуется минимизировать 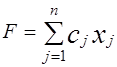 ,
,
при ограничениях
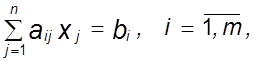 при " x ³ 0.
при " x ³ 0.
Введем векторы:
C = (C1,..., Cn) - вектор оценок,
X = (X1,..., Xn) - вектор переменных,
b = (B1,..., Bm) - вектор ограничений
и матрицу
A = 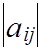
размером (m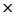 n) - матрицу коэффициентов ограничений.
n) - матрицу коэффициентов ограничений.
Тогда задача ЛП будет иметь следующую трактовку:
минимизировать F=CX
при условиях AX = b, X 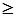 0.
0.
Эту задачу можно записать в матричной форме:
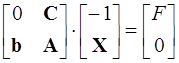

Введем обозначение:
А*= 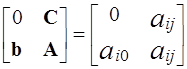 - здесь матрица A * размером (m+1)(n+1).
- здесь матрица A * размером (m+1)(n+1).
Согласно выше приведенной методике находят разрешающий элемент aks.
Следующий шаг симплекс-метода - процедура исключения Гаусса, которая позволяет сделать все коэффициенты в s - м столбце, кроме aks , нулевыми, aks - равным единице.
Для симплекс-метода в матричной форме итерация симплекс-метода эквивалентна умножению матричного уравнения слева на следующую квадратную матрицу:
|
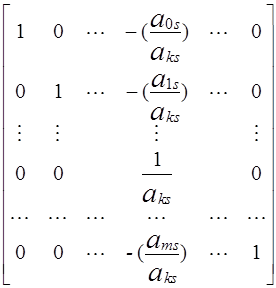 , где k
, где k 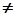 0; s
0; s 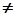 0.
0. Если все столбцы матрицы A разделить на базисные B и небазисные N, то задачу ЛП можно записать так:
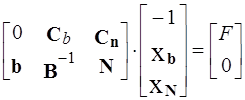 ,
,
где Cb и CN - соответствующие компоненты вектора C, Xb, XN - базисные и небазисные переменные.
Для выбора начальных базисных переменных xb следует умножить уравнение слева на матрицу:
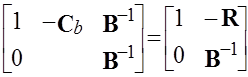
где R= Cb B-1 .
В результате получим
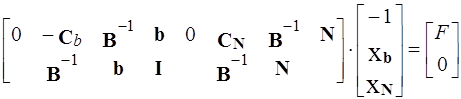 ,
,
где I - единичная матрица.
Отсюда следует, что относительные оценки при небазисных переменных
cj = cj - Cb B-1 aj = cj - Raj.
Базис будет допустимым, если свободные члены при базисных переменных будут неотрицательными, т.е. B-1b ³ 0.
Если cj ³ 0 для 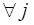 , то базис является оптимальным решением задачи. Вектор
, то базис является оптимальным решением задачи. Вектор 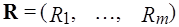 называют вектором текущих цен. Каждая строка умножается на вектор R и вычитается из строки коэффициентов стоимости, для того чтобы исключить коэффициенты стоимости при базисных переменных.
называют вектором текущих цен. Каждая строка умножается на вектор R и вычитается из строки коэффициентов стоимости, для того чтобы исключить коэффициенты стоимости при базисных переменных.
Если задача ЛП задана не в канонической форме, т.е.
минимизировать F=CX
при условиях AX 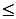 b,
b, 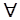 X
X 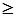 0,
0,
то, вводя слабые переменные, их можно записать в виде
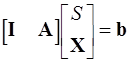
Метод исключения по строкам для матрицы 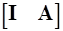 эквивалентен умножению этой матрицы слева на B-1, где B - базис подматрицы A, тогда
эквивалентен умножению этой матрицы слева на B-1, где B - базис подматрицы A, тогда
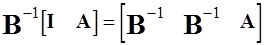 ,
,
т.е. матрица, получаемая на месте единичной I, будет матрицей, обратной для текущего базиса. Относительные оценки, расположенные над единичной матрицей, будут
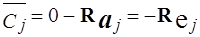 ,
,
поскольку 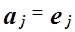 - единичные векторы.
- единичные векторы.
Так как F= CbB-1b = Rb, текущее значение целевой функции равно произведению вектора текущих цен матрицы A на исходный вектор b.
Пример. F = 5X1 + 6X2 + 3X3 + 4X4 + 5X5 ® min
при ограничениях
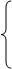 2X1 + 3X3 + 4X4 + 2X5 = 10,
2X1 + 3X3 + 4X4 + 2X5 = 10,
3X2 + 3X4 + 6X5 = 9,
|
Для данного примера матрица A* будет иметь вид
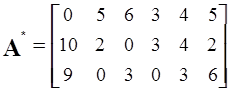 .
.
Пусть X1 и X2 - базисные переменные.
Матрица B имеет вид
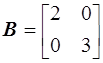 .
.
Тогда обратная матрица B-1 имеет следующий вид
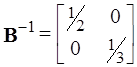 .
.
Напомним, что 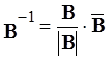 , где
, где 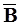 присоединенная матрица, составленная из алгебраических дополнений элементов bik определителя
присоединенная матрица, составленная из алгебраических дополнений элементов bik определителя 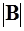 матрицы B.
матрицы B.
Определитель 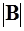 равен:
равен:
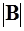 =
= 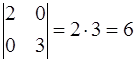 .
.
Следовательно, матрица B неособенная.
Алгебраические дополнения элементов определителя 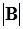 имеют следующие значения:
имеют следующие значения:
b11 = 3, b12 = 0, b12 = 0, b22 = 2; т.е. 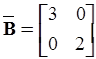 .
.
Умножив 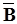 на
на 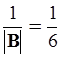 , находим обратную матрицу:
, находим обратную матрицу:
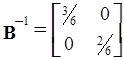 .
.
Вектор текущих цен будет
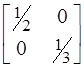 R = CbB-1 =
R = CbB-1 = 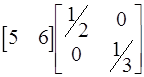 =
= 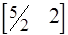 .
.
Напомним, что Cb - базисные компоненты вектора C:
Cb = 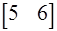 .
.
Тогда 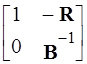 =
= 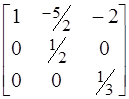 .
.
Для выбора начального базиса нужно матрицу A* умножить слева на матрицу
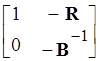 ,
,
получим
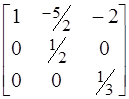
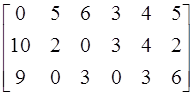 =
=

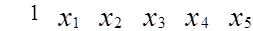


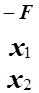
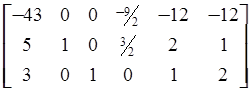 .
.
Разрешающий элемент находится в квадрате.
Итерация симплекс-метода эквивалентна полученной таблице, умноженной слева на следующую матрицу:
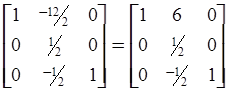 .
.
Эта матрица получена из матрицы (1.23)
Здесь aks = 2;
a11 = 1; a12 = - a0s / aks = - 12/2 = - 6;
a13 = 0; a21 = 0; a22 = 1/ aks = 1/2; a23 = 0;
a31 = 0; a32 = - ams / aks = -1/2; a33 = 1.
Тогда имеем
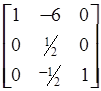
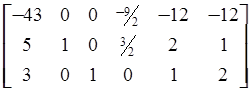 =
=


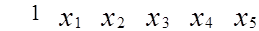

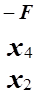
 (1.24)
(1.24)
Разрешающий элемент помещен в квадрат.
Следующая итерация симплекс-метода равносильна умножению слева на матрицу
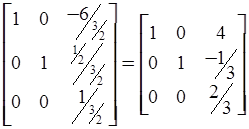 .
.
Тогда
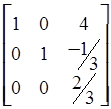
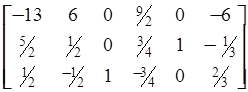 =
=

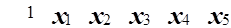

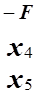
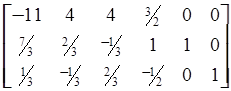 .
.
Следовательно, F min =11; X4 =7/3; X5 =1/3; X1=X2=X3 =0.
Модифицированный симплекс-метод ( МСМ ) отличается от обычного симплекс-метода ( СМ ) тем, что в СМ все элементы симплекс-таблиц пересчитываются на каждой итерации и при получении очередной таблицы, все предыдущие таблицы, включая исходную, не сохраняются. В МСМ сохраняется исходная таблица, а на каждой итерации определяются: строка относительных оценок C, вводимых в базис 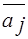 , и текущее значение вектора правых частей ограничений
, и текущее значение вектора правых частей ограничений 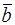 . Для того чтобы определить все элементы таблицы после j- й итерации СМ, достаточно знать матрицу B-1, соответствующую этой таблице, исходную матрицу и индексы текущих базисных переменных. Тогда текущий вектор R = Cb B-1 (индексы текущих базисных переменных определяют, какие элементы вектора оценок из исходной таблицы входят в вектор Сb);
. Для того чтобы определить все элементы таблицы после j- й итерации СМ, достаточно знать матрицу B-1, соответствующую этой таблице, исходную матрицу и индексы текущих базисных переменных. Тогда текущий вектор R = Cb B-1 (индексы текущих базисных переменных определяют, какие элементы вектора оценок из исходной таблицы входят в вектор Сb); 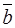 = B-1b , где b берется из исходной таблицы, а любой столбец новой таблицы
= B-1b , где b берется из исходной таблицы, а любой столбец новой таблицы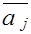 = B-1 a j, где a j - столбец исходной таблицы.
= B-1 a j, где a j - столбец исходной таблицы.
Пусть задана теперь исходная таблица B-1 , соответствующая таблице i -й итерации. Для того чтобы получить матрицу B-1 , соответствующую (i+1)- й итерации, надо определить небазисный столбец i -й таблицы 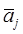 , который должен быть введен в базис. Из СМ следует, что
, который должен быть введен в базис. Из СМ следует, что 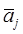 может быть введен в базис, если Cj <0. Таким образом, необходимо вычислить Сj для i -ой таблицы, выбрать среди них
может быть введен в базис, если Cj <0. Таким образом, необходимо вычислить Сj для i -ой таблицы, выбрать среди них 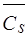 <0, а затем вычислить
<0, а затем вычислить
a S = B-1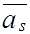 и
и 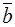 = B-1b (
= B-1b (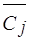 = Cj - Ra j).
= Cj - Ra j).
Найдя разрешающий элемент и используя элементы векторов 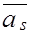 и
и 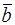 , находим матрицу B-1 для следующей таблицы.
, находим матрицу B-1 для следующей таблицы.
Пример. Модифицированным симплекс-методом минимизировать
F = 5X1 + 6X2 + 3X3 + 4X4 + 5X5 ® min
при ограничениях:
 2X1 + 3X3 + 4X4 + 2X5 = 10,
2X1 + 3X3 + 4X4 + 2X5 = 10,
3X2 + 3X4 + 6X5 = 9,
|
Выбрав в качестве базисных переменных X1 и Х2, получили следующую задачу: F = 43 - 9/2X3 - 12X4 - 12X5
при условиях
 X1 + 3/2X3 + 2X4 + X5 = 5,
X1 + 3/2X3 + 2X4 + X5 = 5,
X2 + X4 + 2X5 = 3,
|
 Эта задача равносильна следующей: максимизировать Х0= -F при условиях
Эта задача равносильна следующей: максимизировать Х0= -F при условиях
Х0 - 9/2Х3 - 12Х4 - 12Х5 = - 43,
Х1 + 3/2Х3 + 2Х4 +Х5 = 5,
X2 + Х4 + 2Х5 = 3,
|
Исходная таблица имеет вид
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | |
| X0 | -9/2 | -12 | -12 | -43 | |||
| X1 | 3/2 | ||||||
| X2 |
Для исходной матрицы В будет единичной матрицей, т.е. B=I. Поэтому B-1=I. Вектор текущих цен
R = Cb B-1;
R =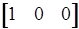
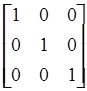 =
= 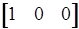 .
.
Текущие оценки в этом случае будут Cj = Raj, поэтому
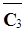 =
= 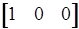
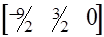 = - 9/2;
= - 9/2;
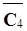 =
= 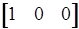
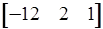 = - 12;
= - 12;
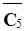 =
= 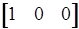
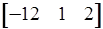 = - 12.
= - 12.
Таким образом, в базис может быть введен вектор 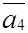 , причем:
, причем:
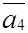 = B-1 a 4 =
= B-1 a 4 = 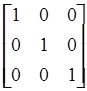
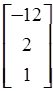 =
= 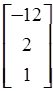 .
.
Текущий вектор правых частей
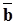 = B-1 b =
= B-1 b = 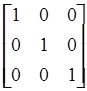
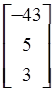 =
= 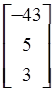 .
.
Находим минимум среди отношений элементов вектора правых частей 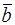 и соответствующего положительного элемента вектора
и соответствующего положительного элемента вектора 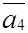 :
:
min 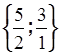 =
= 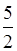 .
.
Отсюда видно, что из базиса должен быть исключен вектор 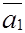 . Исключения по строкам с разрешающим элементом
. Исключения по строкам с разрешающим элементом 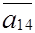 = 2 эквивалентно умножению слева на матрицу
= 2 эквивалентно умножению слева на матрицу
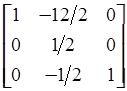 =
=  .
.
После умножения получим



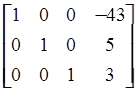 =
=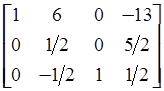 .
.
Обращением нового базиса (Х0, Х4, Х2) будет матрица
B-1 = 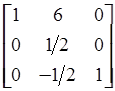 ;
;
R = 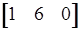 ;
;
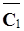 = Ra1 =
= Ra1 =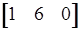
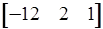 = 6;
= 6;
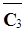 = Ra3 =
= Ra3 =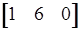
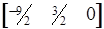 = 9/2;
= 9/2;
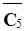 = Ra5 =
= Ra5 =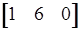
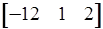 = - 6.
= - 6.
Разрешающим будет 5-й столбец. В базис вводим столбец 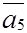 :
:
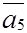 =
= 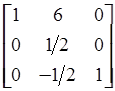
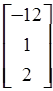 =
=  ;
;
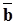 =
= 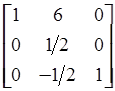
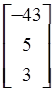 =
= 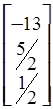 .
.
Находим min 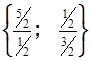 . Следовательно, из базиса выводим вектор
. Следовательно, из базиса выводим вектор 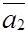 , умножая слева на матрицу
, умножая слева на матрицу
 =
= 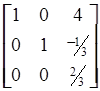 .
.

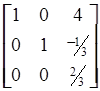
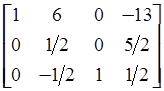 =
= 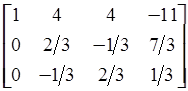 .
.
Обращением нового базиса (Х0, Х4, Х5) будет матрица B-1 .
B-1 = 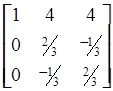 ;
;
R = 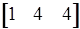 ;
;
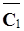 = Ra1 =
= Ra1 =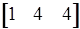
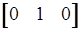 = 4 > 0;
= 4 > 0;
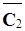 = Ra2 =
= Ra2 =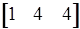
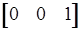 = 4 > 0;
= 4 > 0;
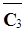 = Ra3 =
= Ra3 =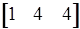
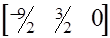 = 3/2 > 0.
= 3/2 > 0.
Следовательно, получаем оптимальное решение:
X0 = - F = - 11; X1 = X2 = X3 = 0;
X4 = 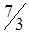 ; X5 =
; X5 = 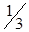 .
.
 2014-02-09
2014-02-09 1961
1961