Метод потенциалов для решения ТЗ

Таблица 1.12

Транспортная задача

Одной из частных задач ЛП является транспортная задача (ТЗ), состоящая в наиболее рациональном закреплении станций отправления к станциям назначения. При этом в качестве критерия оптимальности обычно берется либо стоимость перевозок требуемого количества груза, либо минимальное время его доставки. Важность этой задачи для практики и специфика получающихся ограничений позволили разработать более эффективные по сравнению с симплекс-методом алгоритмы решения. К ним можно отнести распределительный метод, метод дифференциальной ренты, метод потенциалов, венгерский алгоритм и т. д.

Существуют матричная и сетевая постановки транспортной задачи.

Для данной методики в качестве критерия оптимальности принимаем минимизацию стоимости всех перевозок.

Перейдем к более точной формулировке задачи.

Пусть на m станциях отправления А₁, А₂,..., А_m имеется соответственно а₁, а₂,..., а_m единиц однородного груза. Этот груз необходимо доставить по железной дороге в n станций назначения В₁, В₂,..., В_n . В каждую станцию назначения необходимо завезти соответственно b₁, b₂,..., b_n единиц груза. Стоимость перевозки единиц груза (тариф, издержки, транспортные расходы) из станций отправления А_i на станцию назначения В_j считается известной и равной С_{i j}. Матрицу С = (С_ij) будем называть матрицей стоимостей (тарифов). Требуется составить такой план перевозок X = (х_{i j} ), при котором общая (суммарная) стоимость транспортных издержек будет минимальная. Эти условия ТЗ удобно записать в виде таблицы 1.12, называемой матрицей перевозок.

Станции отправления	Запасы грузов	Станции назначения
		B1	B2	...	Bj	...	Bn
		Потребности в грузе
		b1	b2	...	bj	...	bn
A1	a1			...		...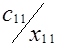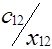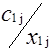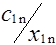
A2	a2			...		...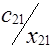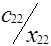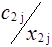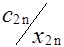
...	...	...	...	...	...	...	...
Ai	ai			...		...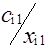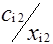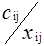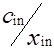
...	...	...	...	...	...	...	...
Am	am			...		...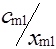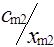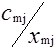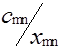

Каждая строка матрицы перевозок соответствует определенному пункту отправления, а каждый столбец - определенному пункту назначения.

Клетки матрицы перевозок, разделенные на две части - верхнюю и нижнюю, соответствуют маршрутам перевозок, число маршрутов (mxn). В верхних отделениях клеток записывают стоимости перевозок единицы груза по каждому маршруту С_{i j}, а в нижних - элементы решения, показывающие количество единиц груза, планируемое к перевозке из i-го пункта отправления в j-й пункт назначения, которое обозначается через x_ij.

Под планом перевозок, состоящим из mxn чисел x_ij (i = 1,m, j= 1,n), понимается совокупность перевозок, обеспечивающая все потребности пунктов назначения за счет вывоза всего груза из пунктов отправления.

Любой план перевозок определяется совокупностью чисел x_ij, т.е. перечислением величин перевозок, совершаемых по каждому из маршрутов.

Эти числа должны удовлетворять следующим условиям:

1. Из каждого пункта отправления должен вывозиться весь имеющийся там груз.

x ₁₁ + x ₁₂ +... + x _1n = a ₁ ,

(1.25)

x ₂₁ + x ₂₂ +... + x _2n = a ₂ ,

...

x _m1 + x _m2 +... + x _mn = a _m;

или 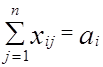, i = 1, m, .

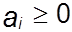2. В каждом пункте назначения должна удовлетворяться вся потребность в рассмотренном грузе.

x ₁₁ + x ₂₁ +... + x _m1 = b ₁,

(1.26)

x ₂₁ + x ₂₂ +... + x _m2 = b ₂,

...

x _m1 + x _m2 +... + x _mn = b _m ;

или 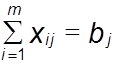, j = 1,n, .

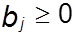3. Движение грузов должно происходить от станций отправления на станции назначения.

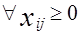; i= 1, m; j= 1,n. (1.27)

Подсчитаем общую стоимость перевозок по плану (табл. 1.12).

По маршруту, соединяющему i-й пункт отправления и j-й пункт назначения, перевозится x_ij единиц груза, а стоимость перевозки по данному маршруту пропорциональна количеству единиц перевозимого груза, т.е. она равна произведению c_ij x_ij единиц. Отсюда суммарная стоимость перевозок по всем маршрутам может быть записана так:

F= c₁₁x₁₁ + c₁₂ x₁₂ +... + c_ij x_ij +... + c_mn x_mn

или F= .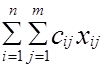

Решение транспортной задачи заключается в нахождении такого плана перевозок, при котором суммарная стоимость перевозок была минимальной F= 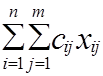min.(1.28)

При решении транспортной задачи условия (1.25) и (1.26) могут быть выполнены, если общее количество груза на станциях отправления равно суммарной потребности в этом грузе на всех станциях назначения (баланс наличия и потребления). Это может быть записано в виде равенства .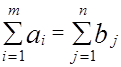

В этом случае транспортная задача разрешается и называется закрытой.

Теперь мы в состоянии записать математическую модель ТЗ.

Найти матрицу перевозок X = 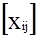, доставляющую минимум целевой функции F= .

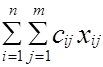при следующих ограничениях:

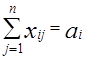, i = 1, m, ,

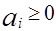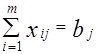, j = 1, n, ,

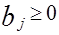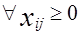, i= 1, m; j= 1,n.

Нетрудно усмотреть, что нами получена каноническая задача ЛП(КЗЛП). Более того, коэффициенты при всех m x n переменных x _ij равны 1, а каждая из переменных входит лишь в два уравнения.

На практике приходится решать задачи, в которых наличие груза и потребность в нем не являются сбалансированными, т.е.

.

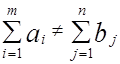Такая транспортная задача называется открытой. Методы ее решения в настоящее время слабо разработаны на теоретическом уровне, поэтому при решении открытой транспортной задачи на практике ее обычно приводят к закрытой форме.

Рассмотрим наиболее часто встречающиеся случаи отклонения от открытой модели.

Случай 1. ТЗ с избытком запасов

Требуется найти оптимальный план перевозок при условии, что суммарные запасы груза больше общих потребностей:

.

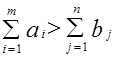Для приведения такой задачи к закрытой модели введем некоторую фиктивную станцию назначения B_n+1 с потребностями:

b_n+1 =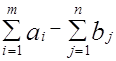

и будем предполагать, что стоимость перевозки единицы груза из любой станции A_i в фиктивную станцию B_n+1 равно нулю, т.е. C_in+1 = 0,

i= 1, m.

Таким образом, отправление какого-то количества груза x_i0 со станции A_i на станцию B_n+1 попросту будет означать, что на станции A_i осталось неотправленым x_i0 единиц груза.

Оптимальное решение этой задачи является также оптимальным решением исходной задачи.

Случай 2. ТЗ с избытком заявок.

Требуется найти оптимальный план перевозок при условии, что суммарные запасы меньше общих потребностей:

.

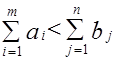В этом случае полное удовлетворение всех станций назначения B_j невозможно. Следовательно, перевозки необходимо организовать так, чтобы наиболее важные станции обеспечивались грузом в первую очередь и суммарные издержки (суммарный штраф за недопоставку груза) были минимальными.

Пусть r _ij - величина ущерба (штраф), который измеряется в тех же единицах, что и стоимость перевозки c _ij , приходящегося на одну единицу недопоставленного в пункт B_j груза.

Для приведения такой задачи к закрытой модели вводится фиктивная станция отправления A_m+1 с запасами:

a _m+1 = .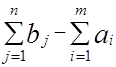

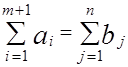= M, M> 0.

Будем полагать, что стоимость перевозок единицы груза между любой станцией B_j и фиктивной станцией A_m+1 равна нулю, т.е.

C_{m+1 j} = 0; j = 1, n.

Далее, минимизируются общие затраты:

F = ,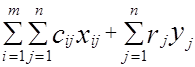

где y _j - величина недопоставки на станцию B_j , определяется как

y_j = B_j - 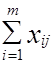; j = 1, n.

При решении задачи величина штрафа задается.

Случай 3. ТЗ с поиском максимума линейной формы

Перейдем к форме F₁ = - F и найдем план X₁*, доставляющий ей минимум. Тогда X* будет оптимальным и для исходной задачи, причем max F = - F1 (X*).

Случай 4. ТЗ с запретными маршрутами

Это такие задачи, в которых нельзя перевозить груз из некоторых пунктов отправления A_i в некоторые пункты назначения B_j. В этом случае стоимости соответствующих перевозок полагаем равными достаточно большому числу. Тогда при отыскании оптимального плана соответствующие перевозки будут блокированы.

Случай 5. ТЗ с обязательными поставками

В практике встречаются задачи, в которых дополнительным условием в ограничениях является обязательное обеспечение конкретных перевозок по определенным маршрутам. В этом случае каждую обязательную перевозку X_ij = d_ij реализуем условно, уменьшая на d_ij запасы в A_i и потребности в B_j. Если это сделать не удается, то исходная задача решения не имеет. В противном случае стоимости обязательных поставок полагаем равными достаточно большому числу, решаем полученную задачу и от ее оптимального плана переходим к оптимальному плану исходной задачи.

Случай 6. ТЗ с ограничением снизу

Пусть требуется решить ТЗ, в которой некоторые из перевозок ограничены снизу l_ij 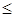x_ij. Тогда следует организовать условные перевозки, уменьшив на l_ij запасы в A_i и потребности в B_j. Если это сделать не удается, то исходная задача решения не имеет, в противном случае решаем полученную задачу и от ее оптимального плана переходим к оптимальному плану исходной ТЗ.

Случай 7. ТЗ с ограничением сверху

Это довольно сложный случай, но и он может быть сведен к определению решения некоторой вспомогательной сбалансированной ТЗ [3].

Одним из эффективных методов решения ТЗ является метод потенциалов, предложенный Л.В. Канторовичем и М.К. Гавуриным. Суть метода заключается в том, что оптимальный план получают способом последовательного приближения, начиная с некоторого предварительного плана перевозок. Этот план может быть выбран произвольно, но с соблюдением условий (1.25), (1.26), (1.27), (1.28).