
Разложим общий поток тепла, поступающий в объём, на составляющие, параллельные осям координат.
Пусть через грань dy ∙ dz входит тепло 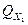 , через грань dх ∙ dz –
, через грань dх ∙ dz – 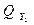 , через грань dy ∙ dx –
, через грань dy ∙ dx – 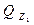 , а через противоположные грани выходит соответственно
, а через противоположные грани выходит соответственно 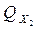 ,
,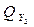 ,
,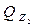 .
.
Количество тепла, введённого в параллелепипед через три грани.
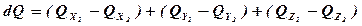
В соответствии с законом Фурье 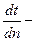 градиент температуры
градиент температуры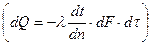 , количество тепла, воспринимаемого гранью
, количество тепла, воспринимаемого гранью 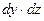 , может быть выражено как
, может быть выражено как

Для количества выведенного тепла в направлении оси Х
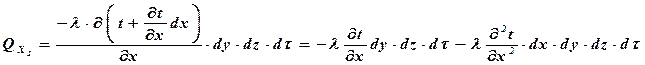
Следовательно, количество тепла, израсходованного на нагрев параллелепипеда тепловым потоком вдоль оси х за время dτ
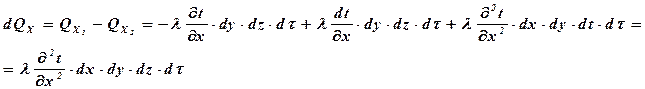
Аналогично для двух других осей
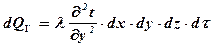
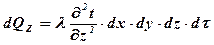
Общее количество тепла, полученное элементарным объёмом
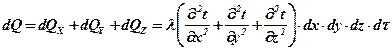 (5.1)
(5.1)
На основе закона сохранения энергии количества тепла, введённого в объём dx·dy·dz, равно изменению его энтальпии (внедрённой энергии – теплосодержанию) и может быть выражено соотношением
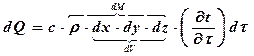 , (5.2)
, (5.2)
где с – теплоёмкость материала параллелепипеда, ρ – плотность,
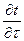 – изменение температуры во времени.
– изменение температуры во времени.
|
|
|
Приравняв правые части уравнений (5.1) и (5.2), получим дифференциальное уравнение теплопроводности Фурье.
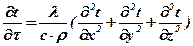 (5.3)
(5.3)
Множитель 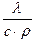 – называется коэффициентом температуропроводности.
– называется коэффициентом температуропроводности.
Обозначим 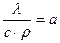 и
и 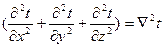 .
.
 2014-02-13
2014-02-13 2269
2269








