Рассмотрим однородное к уравнению (*) п.17.1 уравнение 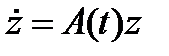 ,
, 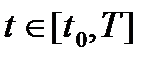 (1).
(1).
Пусть 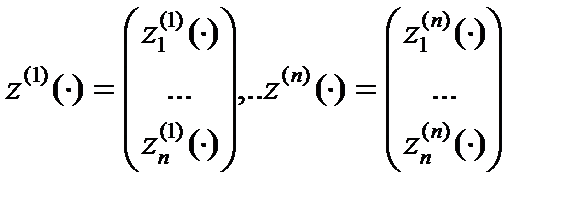 система линейно независимых векторов-решений уравнения (1). Тогда матрица
система линейно независимых векторов-решений уравнения (1). Тогда матрица 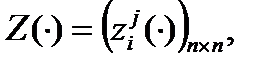
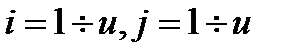 является неособой на
является неособой на 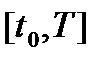 и имеет обратную
и имеет обратную 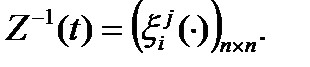 Матрицу
Матрицу 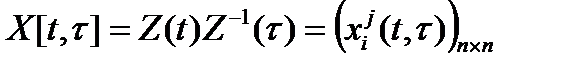
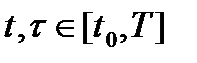 назовем фундаментальной матрицей Коши. Отметим ряд ее свойств:
назовем фундаментальной матрицей Коши. Отметим ряд ее свойств:
1) 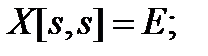 2)
2) 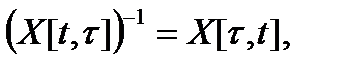
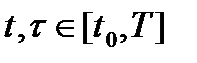 3)
3) 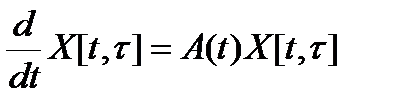 , т.е. столбцы являются линейной комбинацией столбцов Z(t) и являются решением для (1); 4)
, т.е. столбцы являются линейной комбинацией столбцов Z(t) и являются решением для (1); 4) 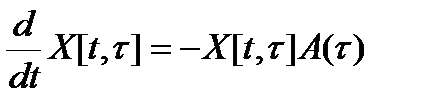
Пусть 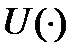 - некоторое уравнение и
- некоторое уравнение и 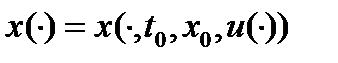 отвечающее ему движение линейного управляемого фундаментального объекта ((*)п.17.1).
отвечающее ему движение линейного управляемого фундаментального объекта ((*)п.17.1).
Теорема1 (Формула Коши). Справедливо равенство
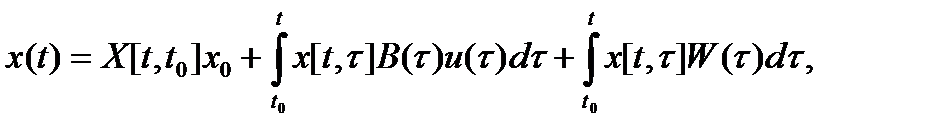
 (2)
(2)
Доказательство. Надо доказать два равенства:
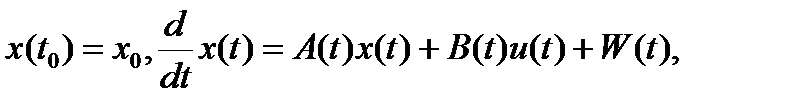
 .
.
Первое следует непосредственно из свойства 1) фундаментальной матрицы Коши, а второе доказывается путем непосредственного дифференцирования правой части равенства (2) по аргументу t:
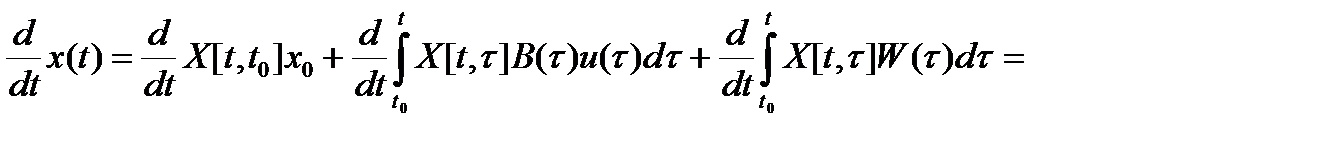
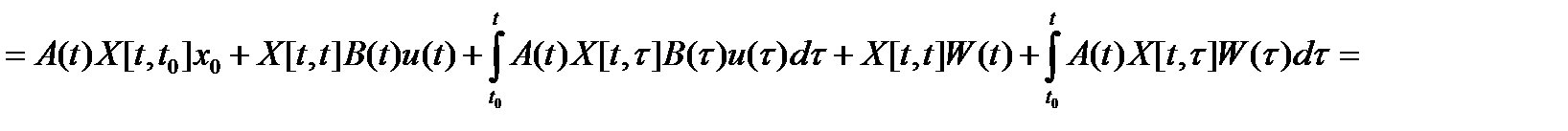
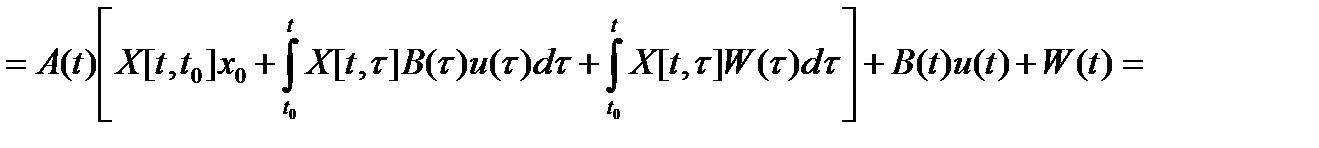
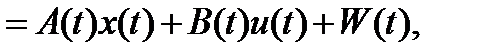
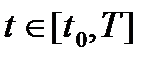 .
.
 2015-01-21
2015-01-21 1055
1055








