2015-01-21
2064
Для стального вала постоянного поперечного сечения (согласно схеме) с двумя зубчатыми колесами (согласно схеме), передающего мощность Р при угловой скорости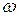 
определить необходимый диаметр вала по двум вариантам: а) используя третью гипотезу прочности; б) используя пятую гипотезу прочности. Принять: 
.
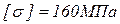Последовательность решения задачи:
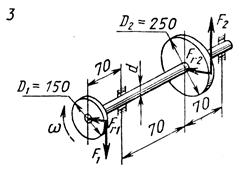
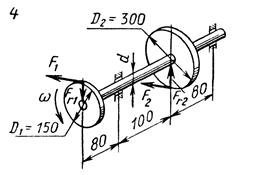
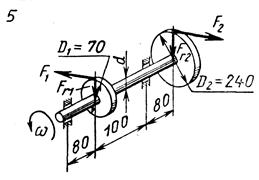
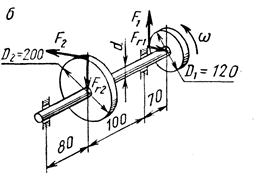
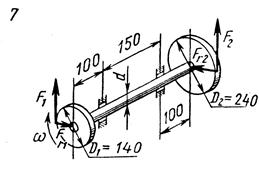
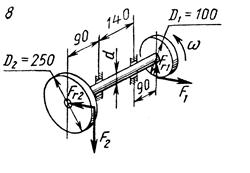
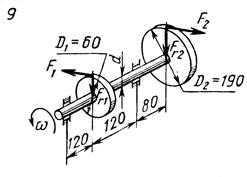
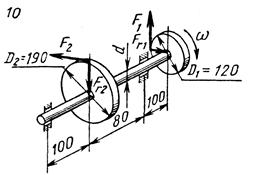
1. Привести действующие на вал нагрузки к его оси, освободить вал от опор, заменив их действие реакциями в вертикальной и горизонтальной плоскостях.
2. По заданной мощности Р и угловой скорости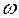 
определить вращающие моменты, действующие на вал.
3. Вычислить нагрузки F1, Fr1, F2, Fr2, приложенные к валу.
4. Составить уравнения равновесия всех сил, действующих на вал, отдельно в вертикальной и горизонтальной плоскостях и определить реакции опор в обеих плоскостях
5. Построить эпюру крутящих моментов,
6. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях (эпюры Мх и Му).
7. Определить наибольшее значение эквивалентного момента по теориям прочности.
|
|
|
8. Считая, что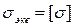 
, определить требуемый диаметр вала.
Таблица 6.5 Варианты заданий к задаче 5
| № схемы (последняя цифра шифра) | Вариант (предпоследняя цифра шифра) | Мощность Р, кВт | Угловая
скорость , с-1
| № схемы (последняя цифра шифра) | Вариант (предпоследняя цифра шифра) | Мощность Р, кВт | Угловая
скорость , с-1
|
Схемы нагружения к задаче 5 (последняя цифра шифра).
|
|
|
| 
|
| 
|
| 
|
| 
|
| 
|
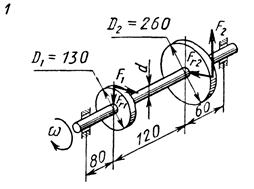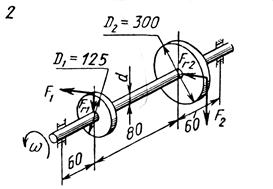ПРИЛОЖЕНИЯ
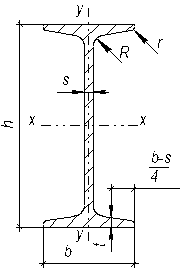
| h — высота двутавра; | Ix, Iy — моменты инерции; |
| b — ширина полки; | Wx, Wy — моменты сопротивления; |
| s — толщина стенки; | Sx — статический момент полусечения; |
| t — средняя толщина полки; | ix, iy — радиусы инерции |
| R — радиус внутреннего закругления | S — площадь поперечного сечения |
| r — радиус закругления полки |
