Для любых векторов  и
и  справедливы следующие свойства скалярного произведения:
справедливы следующие свойства скалярного произведения:
1. свойство коммутативности скалярного произведения  ;
;
2. свойство дистрибутивности  или
или  ;
;
3. сочетательное свойство  или
или  , где
, где 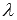 - произвольное действительное число;
- произвольное действительное число;
4. скалярный квадрат вектора всегда не отрицателен  , причем
, причем  тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 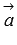 нулевой.
нулевой.
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения  . По определению
. По определению 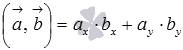 и
и  . В силу свойства коммутативности операции умножения действительных чисел, справедливо
. В силу свойства коммутативности операции умножения действительных чисел, справедливо  и
и  , тогда
, тогда  . Следовательно,
. Следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,  и
и  , откуда следует
, откуда следует

 2015-01-21
2015-01-21 1101
1101
