Уравнение Клапейрона-Клаузиуса для фазового перехода «жидкость-пар»

Для равновесного перехода «жидкость-пар» необходимо одновременно изменять и давление и температуру, поскольку двухфазная однокомпонентная ТС обладает одной степенью свободы.

Получим условие равновесия ТС, рассматривая бесконечно малый цикл Карно при переходе «жидкость-пар» в p-v и T-s координатах:

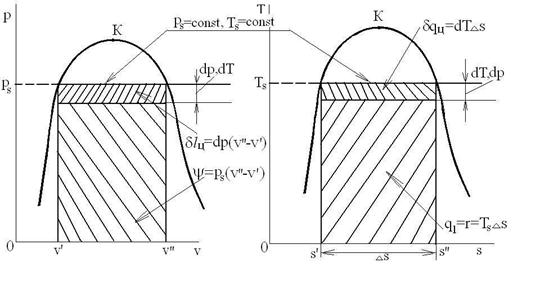
Термический кпд цикла Карно равен:

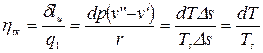. Отсюда имеем:

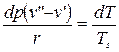, или

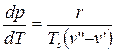. Это уравнение Клапейрона-Клаузиса.

При переходе «жидкость-пар» удельный объем растет, т.е. 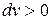и 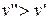, теплота парообразования 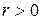и 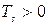. Поэтому величина 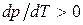, т.е. положительна. Таким образом, давление насыщенного пара над жидкостью для фаз, находящихся в равновесии, всегда возрастает с ростом температуры.

С помощью уравнения Клапейрона-Клаусиуса можно вычислить удельную теплоту парообразования r по известным значениям удельного объема 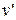и 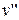и известной зависимости упругости насыщенного пара от температуры 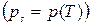, по которой определяется производная 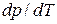. При переходе из твердого состояния в жидкое для большинства веществ 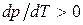. Для воды, висмута и галлия при переходе: «лед-жидкость» удельный объем 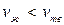и 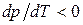. При этом рост давления приводит к уменьшению температуры плавления.

Если жидкость чистая и стенки гладкие, то жидкость может отклоняться от «изотермы-изобары», как это видно из рисунка:

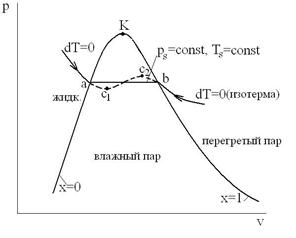
где «аb» - равновесная изобара-изотерма; аС₁С₂b – неравновесные процессы. Таким образом, при изотермическим подводе теплоты 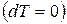в этом случае можно попасть в область перегретой жидкости (т.С₁ – точка минимума кривой, построенной по уравнению Ван-дер-Ваальса), а при изотермическом отводе теплоты – в область кипящей жидкости, когда пар переохлаждается.